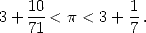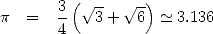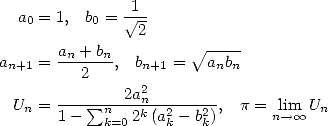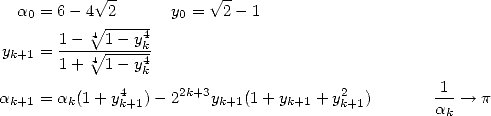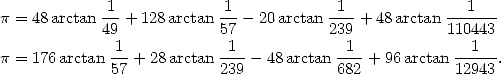|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|

Pi-Story or the history of the number Pi
Very short intro :
A more serious intro !
1
 in the antiquity
in the antiquity
2 Ah finally a bit of analysis ! (18th century - end of 19th century)
3 The computer takes the computer
4 The BBP approach, yet more on
5 A quest with no end ?
References
Associated pages
- Mathematicians' pages (link on each of their names)
- Newton's algorithm
- Multiplication of two bigs integers by Fast Fourrier Transformation
- Finding the n-th digit of Pi without knowing the previous one (Plouffe's method)
- Record of the decimals of Pi throughout the centuries
Very short intro :
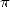 is a constant that finds it's origin from far antiquity.
What a journey travelled up till this day !
is a constant that finds it's origin from far antiquity.
What a journey travelled up till this day !
The history of the constant spreads over four
very distinct periods during which the spirits and the methods
associated to 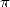 were very differents. We remember basically :
were very differents. We remember basically :
1. 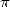 in the antiquity
in the antiquity
* Antiquity - 17th century : the geometric method of Archimedes triumphs
2. Ah, finally some analysis !
* 18th century - start of 20th century: it's a time where it rains discoveries and formulae constantly !
3. The computers take over work...
* 20th century : with the equations by Ramanujan and the computers, we can push at the calculus limits.
4. Let's take a walk in the decimals
* Nearing the millinium, Plouffe starts a revolution !
A more serious intro !
The number 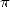 occupies a particular place in the
mathematical world, and always constantly reaffirmed. It can boast to
have occupied the mathematicians mind since antiquity, and as Bergreen
and the Borwein brother [6], the calculation of
it's decimals is probably the only problem to have appeared since the
dawn of mathematics, and that is still current news in today's world.
However, the associated motivations have sensibly evolve throughout the
centuries.
occupies a particular place in the
mathematical world, and always constantly reaffirmed. It can boast to
have occupied the mathematicians mind since antiquity, and as Bergreen
and the Borwein brother [6], the calculation of
it's decimals is probably the only problem to have appeared since the
dawn of mathematics, and that is still current news in today's world.
However, the associated motivations have sensibly evolve throughout the
centuries.
First linked to the pratical and daily need of
the ancients, the evaluations always more precise of the number 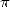 then followed,
nearly like a game, some succesive discovery and fruitful analysis
formulae always more efficients from the renaisance until the 19th
century.
then followed,
nearly like a game, some succesive discovery and fruitful analysis
formulae always more efficients from the renaisance until the 19th
century.
The revolution of computers in the 20th
century will then completely change the game: the attraction of the
calculation did not come from the result itself, but from the method
of obtaining it, from a technical mathematical and algorithmitic point
of view. A new change of direction came since 1966, which tried to put
in relation the analytical expression of 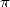 and the profound
structure of its decimals. Of this exploration field at the frontier
of complexity theory was born a few still open conjecture on the
"random" nature of numerous mathematical constant (
and the profound
structure of its decimals. Of this exploration field at the frontier
of complexity theory was born a few still open conjecture on the
"random" nature of numerous mathematical constant (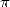 ,
,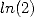 , etc...).
Other consequence that till here was never guessed at, like the
possibility to obtain in certain bases the n-th digit without knowing
the previous one with little time or memory, we have renewed the
attraction of the calculation of digits or decimals of the number
, etc...).
Other consequence that till here was never guessed at, like the
possibility to obtain in certain bases the n-th digit without knowing
the previous one with little time or memory, we have renewed the
attraction of the calculation of digits or decimals of the number 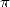 .
.
This page offers to come back on those four
periods (Antiquity, 18th/19th century, 20th century, and since 1966) by
explaining the trails of thoughts and methods of calculations that lead
to knowing more than 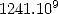 decimals of
decimals of 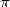 at the start of
this third millenium ! We will achieve this essay by a little look the
actual motivation for the calculation of the decimals of
at the start of
this third millenium ! We will achieve this essay by a little look the
actual motivation for the calculation of the decimals of 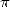 .
.
1 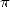 in the antiquity
in the antiquity
With Pi, the time traveling machine is a
reality.... But of course, for more conformability, the modern and
usual language of mathematics are used here... Do not believe that the
Babylonians wrote the numbers in decimals. They didn't even know about
trigeonometry and used base 60 instead of base 10, in fraction
notation (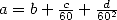 ). Firthermore,
the signs +, =,
). Firthermore,
the signs +, =, ,
, were only invented during the renaissance, the writtings
of the antiquity resembled more to a writting language than anything
else. The egyptians were a bit more advanced and used the decimal
system, manipulating fractions with a numerator of 1, and had invented
a sign + (two legs pointing left) and the - (two legs pointing right).
This being said, let us go back to the origins of the legend...
were only invented during the renaissance, the writtings
of the antiquity resembled more to a writting language than anything
else. The egyptians were a bit more advanced and used the decimal
system, manipulating fractions with a numerator of 1, and had invented
a sign + (two legs pointing left) and the - (two legs pointing right).
This being said, let us go back to the origins of the legend...
1.1
From the height of the pyramids,  looks down unto us !
looks down unto us !
I am sometimes asked in what year we discovered
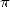 ! I
do not know the answer to this question because it's the result of a
long process. The ancients essentially needed it for the geometry and
measuring the surfaces of the earth, or in architecture, for example to
evaluate the height and the proportion of building. According to the
greek historian Herodote, we could find numerous geometrical relations
in the pyramids of Gizeh, to which he visited towards 450 BC
(that's more than 2000 years after their construction still!). For
example, a construction principle wanted that the aread of each lateral
surface is equal to the squared area of the side equal to the height of
the pyramid (which is accurate to roughly 99.3% for Kheops' pyramid!).
Numerous constants appear in this nearly magical way, since the ratio
of the height on the base of the pyramids with an error of 1,7% . This
remarquable coincidence are sometimes contested but are still
fascinating.
! I
do not know the answer to this question because it's the result of a
long process. The ancients essentially needed it for the geometry and
measuring the surfaces of the earth, or in architecture, for example to
evaluate the height and the proportion of building. According to the
greek historian Herodote, we could find numerous geometrical relations
in the pyramids of Gizeh, to which he visited towards 450 BC
(that's more than 2000 years after their construction still!). For
example, a construction principle wanted that the aread of each lateral
surface is equal to the squared area of the side equal to the height of
the pyramid (which is accurate to roughly 99.3% for Kheops' pyramid!).
Numerous constants appear in this nearly magical way, since the ratio
of the height on the base of the pyramids with an error of 1,7% . This
remarquable coincidence are sometimes contested but are still
fascinating.
The most ancient object where 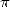 intervenes more
or less implicitely is a babylonian tablette in cuniform writting,
discovered in 1936 and which goes back to the period 1900-1600 B.C. It
evaluated the perimeter of an hexagon to
intervenes more
or less implicitely is a babylonian tablette in cuniform writting,
discovered in 1936 and which goes back to the period 1900-1600 B.C. It
evaluated the perimeter of an hexagon to 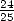 times the
one of a circonscibed circle (either
times the
one of a circonscibed circle (either ![[0,57,36]](../histoire/histoire24x.gif) in
their base
in
their base 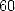 from which we have seconds/minutes left), which comes down to
estimating
from which we have seconds/minutes left), which comes down to
estimating 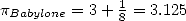 . It's officially the
oldest approximation known of
. It's officially the
oldest approximation known of  !
!
Similarly, to come back to egyptians, the
famous papyrus of Rhind written in hieratic writting and discovered in
1855 by A. H. Rhind at Louxor relating a serie of ancients problems
recopied by the scribed Ahmes. The number affirm that
the area of a disc of diameter
affirm that
the area of a disc of diameter  is equal to 64 , or the square of the diameter
to which we removed
is equal to 64 , or the square of the diameter
to which we removed 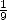 of it's length
of it's length 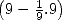 . This comes down to estimating
. This comes down to estimating 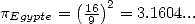 . They
probably came to this idea by aproximating the area of this disk by the
one of an octagon partition in squares and triangles of side 1,
and which then gives an area of 63 (probleme number
. They
probably came to this idea by aproximating the area of this disk by the
one of an octagon partition in squares and triangles of side 1,
and which then gives an area of 63 (probleme number  48). Note that
the Egyptians only work with fractions with the form
48). Note that
the Egyptians only work with fractions with the form 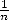 and that they
had opted for the best approximation of this kind this the diminution
of
and that they
had opted for the best approximation of this kind this the diminution
of 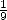 is
better than the diminition of
is
better than the diminition of 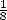 . Notice anyway (let us be fair!) that those
rudimentary tools furnished some value with errors of less than 1%.
This same kind of method will be applied in India (600 B.C) or in China
(150 A.D.)
. Notice anyway (let us be fair!) that those
rudimentary tools furnished some value with errors of less than 1%.
This same kind of method will be applied in India (600 B.C) or in China
(150 A.D.)
In the antiquity, we visibly quickly notices that the ratio between the parameter of a circle and it's diameter was a constant. Furthermore we know that the Egyptians had understood that the ratio linked to the perimeter of a circle and the one link to it's area was the same.
 |
|
|
| Rhind's papyrus conserved at the British Museum (1800-1650 B.C.) |
|
|
| |
We don't know if this was the case for the
Babylonians, or even if those civilisation were conscious of having
obtained a rought value of 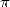 . We need to note that the diffusion of
knoledge at that era was rather reduced, and numerous other
approximation, sometime rather bad one did spring up after the
discovery of those first value. Hence, after the Egyptians and the
Babylonians, it's a bit empty... The Chinesse towards -1200 gives 3 as
a value, this shows a certain lack of research on the subjects! The
Bible, lacking a bit of divine inspiration for the occasion, also gives
3 as a value for
. We need to note that the diffusion of
knoledge at that era was rather reduced, and numerous other
approximation, sometime rather bad one did spring up after the
discovery of those first value. Hence, after the Egyptians and the
Babylonians, it's a bit empty... The Chinesse towards -1200 gives 3 as
a value, this shows a certain lack of research on the subjects! The
Bible, lacking a bit of divine inspiration for the occasion, also gives
3 as a value for 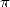 towards -550 B.C... The passage on the founder Hiram and
his chauldron stayed famous, here is the quote "He made the Sea of cast
metal, circular in shape, measuring ten cubits from rim to rim and five
cubits high. It took a line of thirty cubits to measure around it".
30/10=3, no mistakes. We will say a lot later that the quote concerned
the inside contour of the chouldron to calm the debate, but the absence
of precision since founders don't need it seems the oly
justification... Luckly, here are the Greeks that will put a bit of
order in all of this...
towards -550 B.C... The passage on the founder Hiram and
his chauldron stayed famous, here is the quote "He made the Sea of cast
metal, circular in shape, measuring ten cubits from rim to rim and five
cubits high. It took a line of thirty cubits to measure around it".
30/10=3, no mistakes. We will say a lot later that the quote concerned
the inside contour of the chouldron to calm the debate, but the absence
of precision since founders don't need it seems the oly
justification... Luckly, here are the Greeks that will put a bit of
order in all of this...
1.2 Eureka !! : The exhaustion principle with the greeks
The greek mathematicians were often considered as the first to really worry about proofs. The problems that preoccupied them stayed however mainly geometrical. Among them, the problem to build a square of the same area as a circle (the famous squaring a circle) was initiated, at least historicaly, by Anaxagore of Clazomène (500-428 B.C.) during a stay in prison for heriticity (he dared state in particular that the moon only reflected the light of the sun! It was no joking matter back then !). If numerous solution were then proposed, the problem became unsolvable for 23 century when Euclide added the conditions that it could solved uniquely :
- of an unmarque straight edge and a compas,
- in a finite number of stages (implicitely).
The link between those condition and the algebraic properties of numbers that flow from it was properly stated only in 1837 by Pierre Laurent Wantzel :
Theorem 1.1 Numbers finitely defined with the help of the ruler and compas are of size that can be defined by simple algebraic operations (additions, multiplications, extractions of roots....) in other words roots.
Even if numbers defined by radicals are
algebraic (roots of polynomials with coefficients in 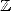 ),
Abel proved in 1824 that not all algebraic numbers can always be
expressed by radicals as soon as the degree of the polynomial reached
5, and Liouville showed in 1851 the existence of non algebraic numbers,
i.e. transcendental. The problem of squaring the circle came quickly
down in the middle of the 19th century to the problem of the
transcendence of
),
Abel proved in 1824 that not all algebraic numbers can always be
expressed by radicals as soon as the degree of the polynomial reached
5, and Liouville showed in 1851 the existence of non algebraic numbers,
i.e. transcendental. The problem of squaring the circle came quickly
down in the middle of the 19th century to the problem of the
transcendence of 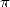 .
.
The distance which seperated the greek
geometric conception and the formal expression of squaring the circle
problem explained the slow growing of the mathematicians toward the
final and rigourous proof of the transcendence of 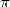 in 1882 by Lindemann , which would nail this old
debated old of more than 23 centuries !
in 1882 by Lindemann , which would nail this old
debated old of more than 23 centuries !
With the tools that the greek had, the solution proposed for the squaring the circle called most of the time for an infinite number of steps like the quadratic of Dinostrate, constructed initially by Hippias d’Elis towards 430 B.C. or even the exhaustion method.
This last one was generally attributed to
Antiphon ( 430
avant J.C.) or Eudoxe of Cnide (408-355 B.C.), and consist of
constructing a polygon whose number of sides will increase until it
became very like a circle.This brilliant idea hit the problem of a lack
of notion of limits in that era. We now know that it's not because a
property is true for all integer 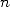 that it is true at the limit (
that it is true at the limit (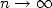 ). In
other words, even if a polygon of side
). In
other words, even if a polygon of side 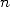 is squarable,
this does not mean that it's limit - the circle - is also,
contrary to Antiphon's idea. The brilliant Euclide (330-275 B.C.) write
nevertheless that by considering a polygon with a great numbers of
sides, we can "make the difference between the area to calculate and
the area of the polygon that have constructed smaller than any positive
quantity pre-assigned, no matter how small" (according to [12]), which is a
conception suprisingly close to the formalisation of limits in
mathematics of the 19th century. He deduce from it that the area of the
circle was proportional to the square of its diameter (Elements 12.2)
is squarable,
this does not mean that it's limit - the circle - is also,
contrary to Antiphon's idea. The brilliant Euclide (330-275 B.C.) write
nevertheless that by considering a polygon with a great numbers of
sides, we can "make the difference between the area to calculate and
the area of the polygon that have constructed smaller than any positive
quantity pre-assigned, no matter how small" (according to [12]), which is a
conception suprisingly close to the formalisation of limits in
mathematics of the 19th century. He deduce from it that the area of the
circle was proportional to the square of its diameter (Elements 12.2)
 |
|
|
| Two pages from Euclide's Elements |
|
|
| |
 |
|
|
| Euclide (365-300 B.C.) |
|
|
| |
We need to wait however for Archimedes
(287-212 B.C.) and his paper “On the measure of the circle” for this
idea to be efficiently applied to the evaluation of 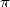 . The first of
these 3 theorems states that the ratio of the area of a disk to the
square of its radius is equal to the ratio of its perimeter to its
diameter. The third problem explicitely states that
. The first of
these 3 theorems states that the ratio of the area of a disk to the
square of its radius is equal to the ratio of its perimeter to its
diameter. The third problem explicitely states that
 |
|
|
| Archimedes (287-212 B.C.) |
|
|
| |
Let us take the exhaustion principle, it
exhibites a formal relation between a polygon of 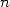 sides with one
of
sides with one
of 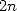 sides
(see Archimedes's page).
Starting from two hexagons respectively inscribed and circonscribed, he
obtained the approximation 1
with two polygons of 96 sided ! This amazing calculation was made with
no algebraic notation, coherant numeration (the greeks used an additive
numerations like the romains), nor the knowledge of trigonometrie, and
with only Euclide's geometry. He formalised it as follow: Let
sides
(see Archimedes's page).
Starting from two hexagons respectively inscribed and circonscribed, he
obtained the approximation 1
with two polygons of 96 sided ! This amazing calculation was made with
no algebraic notation, coherant numeration (the greeks used an additive
numerations like the romains), nor the knowledge of trigonometrie, and
with only Euclide's geometry. He formalised it as follow: Let 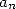 and
and 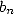 be the semi
perimeters of polygons of
be the semi
perimeters of polygons of 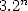 sided respectively circonscribed and
inscribed in a circle of radius 1. The hexagon gives
sided respectively circonscribed and
inscribed in a circle of radius 1. The hexagon gives 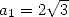 and
and 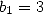 . We then
have the recurrance formulae
. We then
have the recurrance formulae
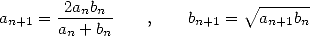 |
(2) |
which gives 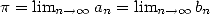 .
Archimedes pushed his calculations up to
.
Archimedes pushed his calculations up to 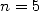 . The case
. The case 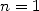 and
and 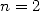 are
illustrated in the picture below.
are
illustrated in the picture below.
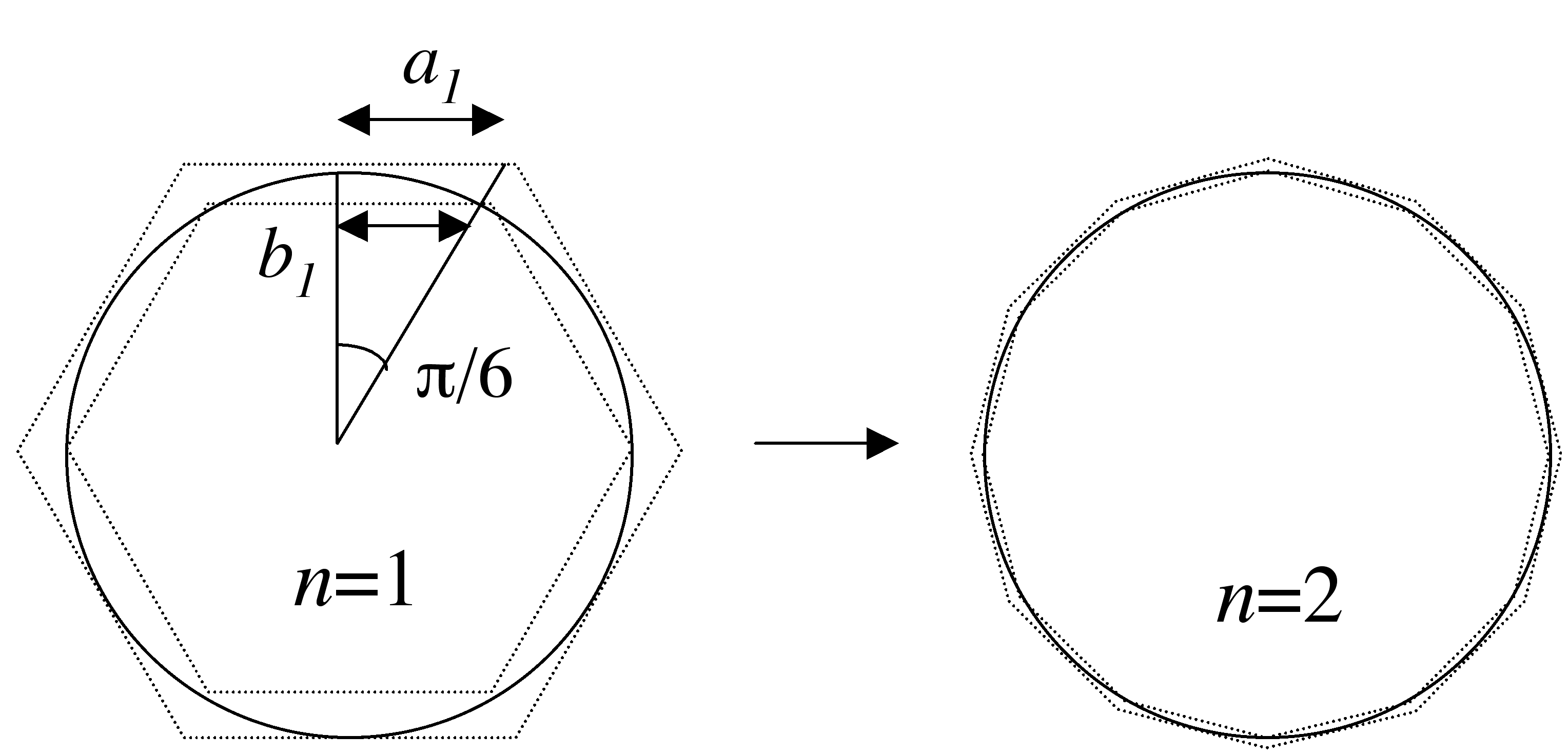 |
|
|
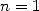 and and 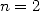 of Archimedes' iteration of Archimedes' iteration |
|
|
| |
The proof of the convergence and the adjacence
of the two sequence is straight forward if we note that 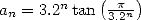 and
and 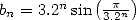 . We hence
obtain
. We hence
obtain
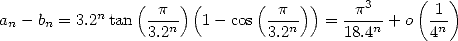 |
(3) |
which assures a number of correct decimals equal
to 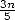 iterations roughly (3 decimals in 5 stages). We will qualify this
convergence to be linear. The brilliance of Archimedes
was already well know in that era, that
Tropfke [25] said
that the value
iterations roughly (3 decimals in 5 stages). We will qualify this
convergence to be linear. The brilliance of Archimedes
was already well know in that era, that
Tropfke [25] said
that the value 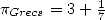 quickly replaced in Alexandria
the old value
quickly replaced in Alexandria
the old value  =
=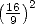 , of more easy use but a lot less precise, and that it
was spread till India and even in China in the 5th century.
Ptolémée improved a bit the result using trigonometric
tables
, of more easy use but a lot less precise, and that it
was spread till India and even in China in the 5th century.
Ptolémée improved a bit the result using trigonometric
tables
1.3 Traveling...
After Archimedes, the mathematician night fall on the East for 1500 years.... It is true that the numerical system of the romains for example is of not much use for calculation (try to multiply LVIII by XCVI !) and they did not leave much behind them in tems of mathematical works. But things happens else where. Even if the asian, arabian or indian mathematicians just applied the same method of Archimedes, or a slight variant for 20 century, they offer better and better approximation. Hence, in India, we also work since Aryabhata offers, towards 500 B.C., 3 exact decimals. But, it was in China where the decimal system was always used, that the progress was faster. Tsu Chung Chih seems to be the first to give the famous fraction 355/113 = 3,14159292... towards 480 A.D. i.e. 6 decimals. The Arabians and Persians are not left behind since in their Hexadecimal, Al Kashi calculated with virtuosity 10 digits i.e. 14 decimals in 1949.... Absolute record !
 |
 |
 |
|
|
|
|
| Aryabhata (476-550) | Tsu Chung-Chi (430-501) | Al-Kashi (1390-1450) |
|
|
|
|
| |
But the decimal notation starts to slowly
impose itself in Europe in the Middle ages and it all natural that the
West wakes up: it's Fibonacci, one of the
few great mathematician of the era and knowledgable in decimal
notation, which illustarate first of all and get 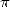 =3,1418...
meah...
=3,1418...
meah...
 |
|
|
| Fibonacci (1175-1250) |
|
|
| |
Note that we did not yet understand precisely the transcendant nature of Pi (which is quite normal...) since Nicolas de Cues said in the 15th century
Regiomontanus will prove (!) that this value is wrong... Nicolas de Cues used a varient of the method by Archimède.  |
|
|
| Nicolas de Cues (1401-1464) |
|
|
| |
From time to time, a few try to be original.
Hence, Descartes
(1596-1650) took the problem the other way and offered his method of
isoperimeters which does not involve the perimeter of polygons but the
diameter of those polygons, whose perimeter is fixed. Viete also derived a first infinite product in
1593 (without proving it, but well, it wasn't usual to in that time!)
by looking at the area and not the perimeter:
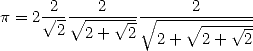 |
(5) |
But the convergence is so slow that he still prefered to use Archimède's method to calculate himself 9 decimals in 1593.
 |
 |
|
|
|
| René Descartes (1596-1650) | Viete (1540-1603) |
|
|
|
| |
With simple 1000 years behind on the Chinese
and Tsu Chung Chih, but it is his name who was remembered,
Adrian Anthonisz does the average of the boxing values calculated by Archimède and refind
355/113=3.14159292... In any case it's what his son claims by
publishing the result in 1625. Those values where hold to be exact for 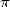 . Since the
greeks, we knew that there exist some numbers more complicated than the
rationals (irrationals) like
. Since the
greeks, we knew that there exist some numbers more complicated than the
rationals (irrationals) like 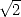 . We felt that
. We felt that 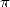 was of more
complex nature, but we still tried to express it as a function of
simpler numbers. During that time, the decimal numeratation quickly
progress the decimal race that became a common sport and the records
did not leave the west...
was of more
complex nature, but we still tried to express it as a function of
simpler numbers. During that time, the decimal numeratation quickly
progress the decimal race that became a common sport and the records
did not leave the west...
Pushing the calculation further than Archimedes, the record in this area belong to
Ludolph Van Ceulen
(1539-1610), who found 20 decimales in 1596 with the help of a polygon
with 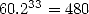 million sides, then 32 decimals with the help of a
polygon of
million sides, then 32 decimals with the help of a
polygon of 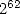 sides in a postum plublication in 1615, so to finally be
attributed and marked on his tombstone 35 decimals in 1621. What an
obsession ! Might as well say he spend his life to this excersice, and
for reward that
sides in a postum plublication in 1615, so to finally be
attributed and marked on his tombstone 35 decimals in 1621. What an
obsession ! Might as well say he spend his life to this excersice, and
for reward that 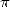 is called von Ceulen's number in Germany
!
is called von Ceulen's number in Germany
!
 |
|
|
| Ludolph Van-Ceulen (1540-1610) |
|
|
| |
In fact there was not much real progress in
this period essentially due to the exclusie use of geometric approach,
which started to find its limit in the calculation of the decimals of 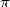 .
.
The squaring of the circle continued, but
started to give true problems... Leaving the geometric era which did
not give any solution, analysis will start looking at it, and we will
see, with success. Note that the Académie
des Sciences in France, had promise a reward for the solution, received
at this period several wrong errors. As "Le petit Archimède",
the best price in this domain is to someone named Liger which start to
prove that 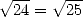 , the rest follows...
, the rest follows...
2 Ah finally some analysis! (18th century - end 19th century)
The great turn happens with the manipulation more and more current of infinite sum and product in the mathematic world at the end of the midle ages.
2.1 The time of arguments
During this perid, some violent arguments
appeared: one of the most famous of them concern Leibniz
(1646-1716) and Newton (1642-1727) who
fighted over the parentship of of the discovery of diferential calculus
and loose a lot of energy.... There are still some who are skeptical
(Rolle, for example, who did not believe in this revolution and will
get angry at Varignon, but still give us one of the most famous thoerem
of this theory), differential calculus will change mathematics
forever... The reults apear rapidly and the research on 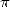 will largely
benifit from it. It's the first time that formulae does not translate
directly the link between the geometry from which we define
will largely
benifit from it. It's the first time that formulae does not translate
directly the link between the geometry from which we define 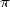 and
and 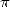 itself. It's in
fact one of the things that in my view is most fascinating in the study
of
itself. It's in
fact one of the things that in my view is most fascinating in the study
of 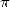 . We are
dealling with big formulae in which it is very difficult to recognise a
geometric property, and yet we find
. We are
dealling with big formulae in which it is very difficult to recognise a
geometric property, and yet we find 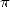 . And the price on the research of a solution
concerning the famous squaring the circle problem offered by the
académie des Sciences always gave a big interest on the
geometry. But all of this was not build in one day
:
. And the price on the research of a solution
concerning the famous squaring the circle problem offered by the
académie des Sciences always gave a big interest on the
geometry. But all of this was not build in one day
:
2.2 The premices of analysis
If there was a mathematician who symbolise a bit this passage of geometry to infinitesimal or the concious of infinity, its Wallis (1616-1703).
 |
 |
|
|
|
| Wallis (1616-1703) | Lord Brouncker (1620-1684) |
|
|
|
| |
His manipulation of infinite series and his
research on the area of a quarter of a circle (starting from the
integral 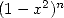 to reach
to reach 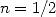 ) pushed him towards horizons yet unknow.
After a proof that stayed famous due to its twist and turns, he find a
very nice formula, the first infinite product of rationals converging
to Pi :
) pushed him towards horizons yet unknow.
After a proof that stayed famous due to its twist and turns, he find a
very nice formula, the first infinite product of rationals converging
to Pi :
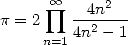 |
(6) |
The convergence is very slow, but it is maybe
the first true serie converging to  coming from analysis. Succeding it is Lord
Brouncker (1620-1684), a friend of Wallis,
who, upon being asked, continue the research on continued fractions and
change Wallis result into a famous
developpment of
coming from analysis. Succeding it is Lord
Brouncker (1620-1684), a friend of Wallis,
who, upon being asked, continue the research on continued fractions and
change Wallis result into a famous
developpment of 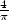 which gives:
which gives:
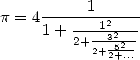 |
(7) |
All of this is centered on infinitesimal but its only with differential calculus that techniques will start to flower.
2.3 The first series
Well before the european, we attributes to
the Indians the first expression of 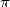 under serie forms since we find in the
writtings of the disciples of Nilakantha Somayaji (1444 - 1545 !) the
formula
under serie forms since we find in the
writtings of the disciples of Nilakantha Somayaji (1444 - 1545 !) the
formula
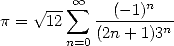 |
(8) |
among eight other. Its simplicity and the speed
of convergence (roughly 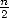 correct decimals for
correct decimals for 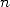 terms) could have lead mathematicians of that era to know some tens of
decimals of
terms) could have lead mathematicians of that era to know some tens of
decimals of 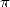 ! However, during this time, as we have seen above, its Al Kashi of Samarkande who did an amazing
feat by calculating 14 decimals of
! However, during this time, as we have seen above, its Al Kashi of Samarkande who did an amazing
feat by calculating 14 decimals of 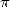 in 1429 with the help of a variant on Archimede's method and in sexagesimal system.
in 1429 with the help of a variant on Archimede's method and in sexagesimal system.
In Europe, it's war! Newton
and his battles against Leibniz and
his 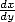 ...
One like the other have at least the merit of habing the vision of
great changes in mathematics. The application of differential calculus
finally allows to obtain or justify the limits of infinite serie as
usual functions (through for example the famous Taylor's formula).
During that time, James Gregory (1638-1675) make Europe benifit from
his discovery of the development in integer series of the arctan
function
...
One like the other have at least the merit of habing the vision of
great changes in mathematics. The application of differential calculus
finally allows to obtain or justify the limits of infinite serie as
usual functions (through for example the famous Taylor's formula).
During that time, James Gregory (1638-1675) make Europe benifit from
his discovery of the development in integer series of the arctan
function
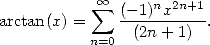 |
(9) |
Applying 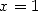 immediatly give a seire for Pi, but,
funnily enough,
Gregory missed it (or more probably, did not see the point in it) and
it only finds itself in the work by Leibniz.
In 1671, it's Abraham Sharp (1651-1742) which use the particular case
immediatly give a seire for Pi, but,
funnily enough,
Gregory missed it (or more probably, did not see the point in it) and
it only finds itself in the work by Leibniz.
In 1671, it's Abraham Sharp (1651-1742) which use the particular case 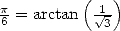 ,
in other words the equation 8,
so to obtain 71 correct decimals of
,
in other words the equation 8,
so to obtain 71 correct decimals of 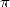 in 1699,
nearly 200 years after Nilakantha ! The development of arcsin was
obtained by Newton towards
1665-1666, who took advantage to calculate 15 decimals of
in 1699,
nearly 200 years after Nilakantha ! The development of arcsin was
obtained by Newton towards
1665-1666, who took advantage to calculate 15 decimals of 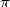 , having
"nothing better to do" as he said it himself.
, having
"nothing better to do" as he said it himself.
 |
|
|
| Newton (1642-1727) |
|
|
| |
The function arctan is a good candidate for
the calculation of the decimals of 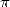 by hand because if we take it from the right
side, we use only rational terms or at worst with a root like in 8. Hence John Machin (1680-1752) easily reaches 100
decimals in 1706 by proposing the now famous formulae
by hand because if we take it from the right
side, we use only rational terms or at worst with a root like in 8. Hence John Machin (1680-1752) easily reaches 100
decimals in 1706 by proposing the now famous formulae
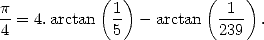 |
(10) |
 |
|
|
| John Machin (1680-1752) |
|
|
| |
The proof or the research of this kind of formulae (from which four other examples are given further by the equation 12, 13, 23 and 24) are obtained by the following rule
Theorem 2.1 Let
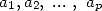 and
and 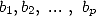 be integers.
be integers. 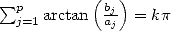 ,
, 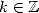 , if and only if
, if and only if 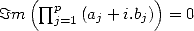 .
.
Proof. If 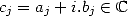 ,
, ![( prod p ) sum p
ln j=1 (aj + i.bj) = j=1 [ln(| cj|)+ i.(arg(cj)+ 2kjp)]](../histoire/histoire110x.gif)
![sum p [ ( (bj) )]
= j=1 ln(|cj|)+ i. arctan aj + 2kjp](../histoire/histoire111x.gif) ,
, 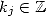 . Consequently
. Consequently 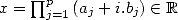 iff
iff 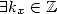 such that
such that 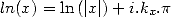 , iff
, iff 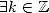 such
that
such
that 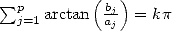 . __
. __
The speed of convergence of these formulae is
constrained by the greatest term 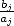 and according to equation 9, we obtain a
linear convergence, in other word a number
and according to equation 9, we obtain a
linear convergence, in other word a number 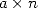 of decimals
by using
of decimals
by using 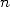 terms of Taylor's expansion of the funtion
terms of Taylor's expansion of the funtion 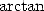 . From now
on, the combination of arctan will be used as a basis for the race to
decimals until 1985 !
. From now
on, the combination of arctan will be used as a basis for the race to
decimals until 1985 !
2.4 The lord of the series
After that the mathematics predominance was installed in England under the impulsion of Newton, they come back to the old continent, in Swiss notably with the Bernoulli and Euler. Its the great analysis period. Euler searches everywhere and never tires of publishing to gives use numerous formulae. The most beautiful of them is with no doubt :
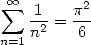
which brings not much to the calculation of decimals but whose simplicity is remarquable... It's proof (see Euler page) is a one of a kind, completly not rigourous, but completly amazing!
 |
|
|
| Euler (1707-1783) |
|
|
| |
A century late, a mathematician which
according to me will indirectly bring the most to the research on 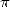 is
Joseph Fourier (1768-1830). His theory
on the decomposition of periodic functions into series, still to be
finalised but who will be the object of rigourousity thorughtout the
19th century, and which is truly revolutionary (so much that certain
mathematicians of the period like Poisson will try to fight back with
loads of energy!). The result allows in fact to simply reprove about
nearly all those formulae of our good old friend Euler.
And of course find new quite interesting ones.
is
Joseph Fourier (1768-1830). His theory
on the decomposition of periodic functions into series, still to be
finalised but who will be the object of rigourousity thorughtout the
19th century, and which is truly revolutionary (so much that certain
mathematicians of the period like Poisson will try to fight back with
loads of energy!). The result allows in fact to simply reprove about
nearly all those formulae of our good old friend Euler.
And of course find new quite interesting ones.
2.5 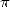 , probably...
, probably...
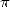 , it's not only geometry and analysis ! Buffon (1707-1788) prove to us with his
famous needle problem that
, it's not only geometry and analysis ! Buffon (1707-1788) prove to us with his
famous needle problem that 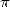 also intervened in the domain of probability.
Of course, this is still due to the definition of
also intervened in the domain of probability.
Of course, this is still due to the definition of 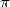 as the
component of the area and the perimeter of a circle, but the theorem by
Cesàro (1859
- 1906) will confirm the inclusion of
as the
component of the area and the perimeter of a circle, but the theorem by
Cesàro (1859
- 1906) will confirm the inclusion of 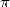 in the
probabilities...
in the
probabilities...
 |
 |
|
|
|
| Buffon (1707-1788) | Cesàro (1859-1906) |
|
|
|
| |
2.6 The challenge
Let us go back to our chronicle race.
Starting from Newton, they are - without
insulting them - more second hand mathematicians who fight for the
record of decimals. Anyway, the number of decimal already calculated in
those time was greater than the needs of mathematicians or physicians.
In fact we estimate that to calculate the circumference of the universe
with the precision of a hydrogen atom, only 39 decimals of 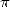 are required !
The motivations are hence more turned towards the search of periodicity
or patterns in the decimals of
are required !
The motivations are hence more turned towards the search of periodicity
or patterns in the decimals of 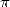 .
The periodicity of a number makes it rational (numbers written as a
fraction
.
The periodicity of a number makes it rational (numbers written as a
fraction 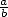 ,
,
 ,
, 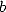 integers).
However, at the turn of the 18th and 19th century, the problem of the
irrationality of
integers).
However, at the turn of the 18th and 19th century, the problem of the
irrationality of 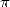 , in other words the impossibility to write it under
rational form, still bother mathematicians. They suspect its true
for a long time but never managed to prove it. With the progress of
analysis, Euler show the irrationality
of
, in other words the impossibility to write it under
rational form, still bother mathematicians. They suspect its true
for a long time but never managed to prove it. With the progress of
analysis, Euler show the irrationality
of  and
Johann Lambert (1728-1777) brings an
answer to the problem of
and
Johann Lambert (1728-1777) brings an
answer to the problem of 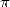 in 1761. His rather heavy proof uses a expansion in
continued fraction of the function
in 1761. His rather heavy proof uses a expansion in
continued fraction of the function 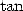 .
Pi is truly irrational
!
.
Pi is truly irrational
!
 |
|
|
| Lambert (1728-1777) |
|
|
| |
In truth the maybe paradoxly more important result that we have found on the spread of the decimals of Pi such that this last remains a mystery to us today. The irrationality indicates that they are not periodic...
There's still the isue of transcendental, in
other words the impossibility to represent 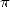 as a
combination of roots and powers of integers, or in equivalent terms,
the fact that
as a
combination of roots and powers of integers, or in equivalent terms,
the fact that 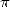 is not the root of any polynomials with integer
coefficients, or even the impossibility of squaring a circle. Even with
all the efforts of many mathematicians (and amateurs that are still
trying to solve the squaring of the circle!), this fort stayed
unbreachable until the end of the 19th century. And the crazy entries
by amateur mathematicians obliged the académie des Sciences to
refuse starting from 1775 the tentavives of proofs on the squaring the
circle , immediate consequence of the transcendance.
is not the root of any polynomials with integer
coefficients, or even the impossibility of squaring a circle. Even with
all the efforts of many mathematicians (and amateurs that are still
trying to solve the squaring of the circle!), this fort stayed
unbreachable until the end of the 19th century. And the crazy entries
by amateur mathematicians obliged the académie des Sciences to
refuse starting from 1775 the tentavives of proofs on the squaring the
circle , immediate consequence of the transcendance.
2.7 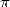 falls in the
shadow
falls in the
shadow
The 19th century comes by... Bizarely,
the most brilliant representant of the scientific genius of the
century, Master Gauss
(1777-1855), even with his uncomparable talent, was not one interested
at all by the research on 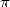 , at least not direcly. We do need to credit
him with a few arctan formulae, but nothing to worship him by !
, at least not direcly. We do need to credit
him with a few arctan formulae, but nothing to worship him by !
Even if Pi continues to appears in many
results, the 19th century is more directed towards algebra and
arithmetics with Galois, Abel, Sophie
Germain and the new theoricians of the non euclidian geometry such as Gauss, Beltrami,
Lobatchevski and Bolyai. The calculation of decimals seems to run out
of breath in the second half of the 19th century. All of this even with
the extraordinary talent of Zacharias Dase, and the enthousiams of a
few like Shanks. Employed by Strassnitsky to calculate 200
decimals, which he did in two month, Dase was the announcer of modern
computers with his fantastic capacity to calculate (he could multiply
in his head two numbers of 100 digits in 8hrs, with breaks, or even
sleeping on it for a whole night, and starting again later!). It needs
to be mentioned that the calculation of decimals by hand seems to have
reach humain limits in 1874 with 707 decimals calculated by Shanks,
which are in fact false starting from the 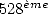 .
Ferguson will notice it nearly 70 years later when comparing them to
the
.
Ferguson will notice it nearly 70 years later when comparing them to
the 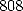 that he obtained in 1948, with the first calculating machines
(addtioners in fact, herited from the principle of those constructed by
Leibniz since 1694). An error that will have hence lasted 92 years
! The room of the palais de la découverte in Paris which proudly
showed off the result by
Shanks decided it was a good idea to be refurnished
!
that he obtained in 1948, with the first calculating machines
(addtioners in fact, herited from the principle of those constructed by
Leibniz since 1694). An error that will have hence lasted 92 years
! The room of the palais de la découverte in Paris which proudly
showed off the result by
Shanks decided it was a good idea to be refurnished
!
 |
|
|
| The room consacred to maths in the Palais de la Découverte in Paris. |
|
|
| |
And since the arctan formulae, we have still have not find in that era a way to go faster and further in the thoery like in practise...
Furthermore, the oldest mathematical problems
was found to be solved in Lindemann in
1882 when he proved the transcendance of 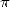 . The squaring
of the circle is hence impossible... How are we going to exist this
impass and remotivate ourself ?
. The squaring
of the circle is hence impossible... How are we going to exist this
impass and remotivate ourself ?
It's from the depth of India at the end of the 19th century that someone grows and will remodel and reshape the century to come.... The era of algorithm and computing will start with him....
3 Computers take the relay
3.1 The Indian breath
During the first half of the 20th century, the mathematicians preoccupation were elsewhere. The theories elaborate by Cantor, Gödel, Kolmogorov, the topologie and the list of 23 problems by Hilbert opens sundunly the horizon which made classical analysis look ancient. It seemed to have found its natural evolution in the study of elliptical integral lead by Legendre, then Gauss, Abel and Jacobi during the first half of the 19th century.
Luckuly a genius born in the depth of India in
1887, Srinivasa Ramanujan , will bring it on himself to
bring new life to research on 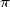 .
.
 |
|
|
| Srinivasa Ramanujan (1887 - 1920). |
|
|
| |
Himself passionated by this constant, he's a self taught man who spend his first 25 years of his life rebuilding the mathematics from a unique work containing 6165 theorems without proofs ("Synopsis of elementary results in pure and applied mathematics” by G.S.Carr). This state of mind lead him to often state results without proving them (which did not mean he did not understand where they came from!). Gifted with exceptional intuition allowed to progress with giant leapsteps in the tehory numbers and modular equation, he discovered some formulae from an other angles like this one published in 1914
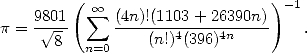 |
(11) |
There exists a funny story about this formula: his proof was nearly completed at the start of the 80s by the Borwein's brothers [7].
 |
 |
|
|
|
|
Borwein Brothers
|
|
|
|
|
| |
|
They just had to justified the 1103
coefficient, it should be an integer, but the length of the calculation
and equations required were horible. Gosper
then effected in 1895 a "blind" calculation of 17 million decimals of 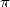 with the help
of this formula. As true as two integer close of less than a unit are
equal, the concordance of the result of the calculation by Gosper with the 10 millions of
decimals already knew at that time constituted of a final proof for the
formula Ramanujan ! We suppose that Ramanujan did the same procedure on a
few decimals.
with the help
of this formula. As true as two integer close of less than a unit are
equal, the concordance of the result of the calculation by Gosper with the 10 millions of
decimals already knew at that time constituted of a final proof for the
formula Ramanujan ! We suppose that Ramanujan did the same procedure on a
few decimals.
The Borwein
will get from the work of Ramanujan
a flow of remarquable algorithm still largely used today in the
calculations of the decimals of 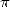 (see paragraph 3.5).
The complexity of the proof of such a formula is such that even a
glance at the results, with no interdemiate proofs, take up a minimum
of several pages in the remarquable work[13]. The reader interested to take a dive
in the passionating world of modular equation, quartic bodies, and
other elliptical integrals can refer themself to the "Bible" [7], of great pedagogie.
(see paragraph 3.5).
The complexity of the proof of such a formula is such that even a
glance at the results, with no interdemiate proofs, take up a minimum
of several pages in the remarquable work[13]. The reader interested to take a dive
in the passionating world of modular equation, quartic bodies, and
other elliptical integrals can refer themself to the "Bible" [7], of great pedagogie.
Ramanujan was noticed by the English mathematician Hardy to which he wrote a letter to in 1913, went to England in 1914 and their fruitful collaboration lasted until 1919.
 |
|
|
| Hardy (1877-1947) |
|
|
| |
He then went back to India were he died the following year, probably due to a lack of victamin. Considered as one of the greatest genius of the 20th cebtury, Ramanujan left notebooks full with loads of formulae in non-standards notations, whose decoding is still hapening today (!), first started by Bruce Berndt, then the Borwein.
3.2 The race to the decimals start again
After Ramanujan who died prematuratly in 1920, its a theoretical desert... until 1976. Hence, during this time, we calculate... After the war, the dawn of calculating machine make the race of decimals progress with giants leaps! Ferguson opens the way in 1946 by obtaining 620 decimals with the help of a desk calculator. The first calculation on computers was given to the famous ENIAC in 1949 which gives 2037 decimals in 70 hours with the help by the formula by Machin 10.
 |
|
|
| ENIAC |
|
|
| |
In 1973, Guilloud and Bouyer reached the first
million decimals on a CDC 7600 with the help of two famous  formulae,
the one by Gauss 12
and of
Störmer 13
formulae,
the one by Gauss 12
and of
Störmer 13
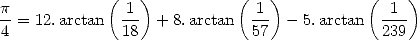 |
(12) |
 |
(13) |
The calculation in binary took respectivaly 22hr11 and 13hr40, and the conversion in decimal base 1h07. A book of 145 pages of decimals pulled from this calculation was qualified at the time as the "most boring book in the world"!
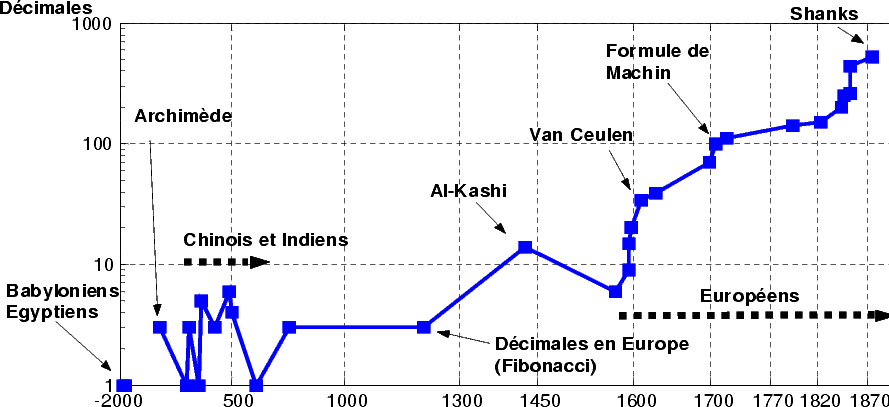
Note that process attach to the race of
decimals is still the same as today: the calculations are fone with two
distinc formulae then compared for the validation of the record. The
figures 1
and 2
shows the evolution of the records of the calculation of the decimals
of 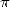 throughout the centuries.
throughout the centuries.
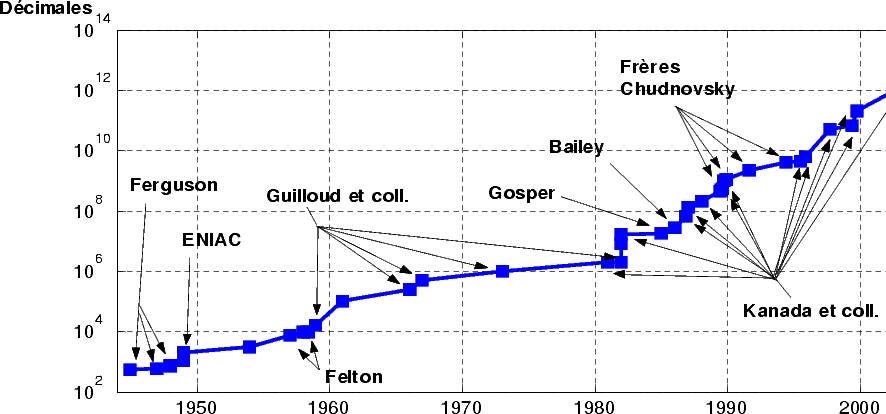
|
3.3 Improvements in algorithms
During this time, the lack of efficient
multiplication algorithm forced to break down each numbers into slices,
for example 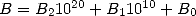 . The multiplication of
numbers of size
. The multiplication of
numbers of size  hence needed a time (or number of operations)
proportional to
hence needed a time (or number of operations)
proportional to  without taking into account the use of memory
proportional to
without taking into account the use of memory
proportional to 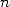 . With no theoretical and algorithmical improvement, the
progress of records of decimals would have been very slow. It was at
this time that things sped up.
. With no theoretical and algorithmical improvement, the
progress of records of decimals would have been very slow. It was at
this time that things sped up.
In 1965, Cooley et
Tukey introduced under it's modern form a method to reduce the
complexity of the calculation of Fourier
series known today under the name of Fast Fourier Transformation [11]. Schönhage and
Strassen get from it an multiplication algorithm for big integers in
complexity 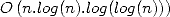 which is much better
than
which is much better
than 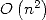 [24]
!
[24]
!
In 1976, Salamin and Brent managed independently to the same algorithm ([23, 8])
which has the extraordinary property of a
quadratic convergence, in other words the number of exact decimals
doubles at each iteration. In fact, Salamin
shows in [23] that
if 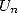 is
the approximation of
is
the approximation of 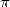 after
after 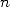 iteration of the algorithm 14,
we get
iteration of the algorithm 14,
we get
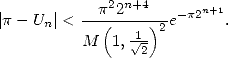 |
(16) |
This upper limits shows that the number of
correct decimals of 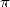 obtained from is stricly greater than
obtained from is stricly greater than 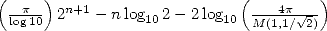 .
. 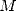 is the arithmetic geometric average (see the page on Salamin).
is the arithmetic geometric average (see the page on Salamin).
 |
|
|
| Richard Brent |
|
|
| |
Let us finaly add that the algorithm by Newton, offered towards 1669 (!), brings back the division and the extraction of square roots to multiplications and also offer a quadratic convergence. Might as well say that all the ingrediants are brought together to make the records explodes !
3.4 World competition
In fact the competition restart in 1981 with
Kanada's team which was probably the first to apply this cocktail of
algorithms (FFT , Newton, Brent-Salamin).
Myioshi and Kanada obtained 2 000 036
decimals in 1981. Strating from this moment, the rythm speeds up, since
the poor Guilloud, which tried to keep his record in 1982 by
calculating 14 decimals more than the Japanese couple, find himself out
of the competition at the end of 1982, when we know 16 777 206 decimals
(Kanada, Yochino and Tamura). The fight then will mainly concern Kanada
and, between 1991 and 1994, the two brothers David and Gregory Chudnovsky which use their own serie
of kind Ramanujan and a computer who
they themself construct the architecture. According to the legend,
their New-York flat contained piles of papers in disorder and was
heated with microchips ! Those isolated mathematicians but with
recognised talent (Gregory is considered as an exceptional genius but
an illness stops him from working at a uni) shows at least that some
first class scientist are interested in the calculation of the decimals
of 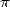 [12].
[12].
3.5 A rainfall of formulae
The 80s see the birth of several very
interesting formulae concerning 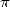 . There was some formulae of kind Ramanujan, some infinite series converging
linearly but fast enough that they are used in the records. These are
refound and explained thanks to the decyphering of the Ramanujan's notebook by Bruce Berndt and the
work of the Borwein
brother and Chudnovsky.
. There was some formulae of kind Ramanujan, some infinite series converging
linearly but fast enough that they are used in the records. These are
refound and explained thanks to the decyphering of the Ramanujan's notebook by Bruce Berndt and the
work of the Borwein
brother and Chudnovsky.
In other part, starting from modular equations implied that the theta functions (whose algorithm by Brent-Salamin was a particular case), the Borwein brothers showed that we can construct algorithms that converges to any speed (quadratic, quartic, quintic...) towards Pi even if the complexity of the calculations increases as a consequence. A good compromise seemed to be the following formula, with quartic convergence [7] :
It was used for the first time by Bailey then Kanada in 1986. Bailey used 12 iterations on a CRAY-2 to calculate 29 360 000
decimals of 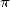 (in fact 45 millions are possible at that stage). It is ammusing to
notice that there only need 100 multiplication, division and extraction
of roots to reach it !
(in fact 45 millions are possible at that stage). It is ammusing to
notice that there only need 100 multiplication, division and extraction
of roots to reach it !
From 1982 to 2002, it is still formulae by Ramanujan (like 11),
the algorithm by Brent-Salamin (14) or a
variant, as well the quartic algorithm of Borwein
(17) which were
used in the race of the calculation of decimals of 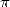 . The first
billion were obtained by the Chudnovsky
brothers in 1989 and, with this method, Kanada, always him, reached
206 billion decimals of
. The first
billion were obtained by the Chudnovsky
brothers in 1989 and, with this method, Kanada, always him, reached
206 billion decimals of 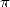 in 1999. Of course, Pi having an infinite number of
decimals, it's not even a drop of water, but the mathematicians hoped
still find, like the Chudnovsky brothers,
some irregularity or property in the decimals of our favourite
constant...
in 1999. Of course, Pi having an infinite number of
decimals, it's not even a drop of water, but the mathematicians hoped
still find, like the Chudnovsky brothers,
some irregularity or property in the decimals of our favourite
constant...
 |
|
|
| Chudnovsky Brothers |
|
|
| |
 |
|
|
From left to right, Salamin,
Kanada, Bailey and Gosper in 87. Ah, the crazy night betweens friends
on  ! ! |
|
|
| |
4 BBP
approche, more new stuff on 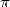
4.1 How to progress ?
The multiplication, the division and
extraction of roots now can be done in a nealry linear time, and
knowing that we can not have less than a complexity 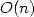 , we can not
expect much more significant advance from this angle. We have seen that
some extremly efficient algorithms existed for the calculation of the
decimals of
, we can not
expect much more significant advance from this angle. We have seen that
some extremly efficient algorithms existed for the calculation of the
decimals of 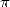 .
Are we then doomed to see the record fall in function to the
progression of computer performances? Yes and no!
.
Are we then doomed to see the record fall in function to the
progression of computer performances? Yes and no!
The mathematicians often surprises where we least expect it. This is how on the 19th september 1995 at 0hr29 (!), after months of research in the dark, Simon Plouffe, David Bailey and Peter Borwein of Vancouver discovered the formula apparently normal and simple
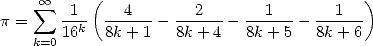 |
(18) |
called since then the BBP formula. The proof is
nearly immediate if we notice that 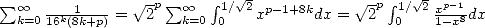 then by calculating the equivalent integral to 18. Euler himself could have discovered it. In
fact, it is to this day one of the most famous example of experimental
maths since this formula was discovered by the algorithm PSLQ of
research on linear relation between numbers. This encouraged the number
of amateurs in mathematicians to start the research of such formulae
thanks to PSLQ or LLL, a similar algorithm implemented on the Pari-GP software.
then by calculating the equivalent integral to 18. Euler himself could have discovered it. In
fact, it is to this day one of the most famous example of experimental
maths since this formula was discovered by the algorithm PSLQ of
research on linear relation between numbers. This encouraged the number
of amateurs in mathematicians to start the research of such formulae
thanks to PSLQ or LLL, a similar algorithm implemented on the Pari-GP software.
 |
|
|
| Simon Plouffe |
|
|
| |
But our three canadian mathematician noticed
above all that this expression is very close to a decomposition in base
16 of 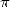 . In
the article [3] of 1996
that is now famous, they show that we can use 18
to reach
. In
the article [3] of 1996
that is now famous, they show that we can use 18
to reach 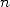 -th
digit of
-th
digit of 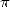 in base
in base 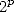 (all the more in base 16) without calculating any of the previous, all
of this in a nearly linear time
(all the more in base 16) without calculating any of the previous, all
of this in a nearly linear time 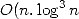 ) and memory
) and memory 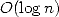 !! The
memory required being minimal, they applied immediatly this result to
calculate the
!! The
memory required being minimal, they applied immediatly this result to
calculate the 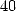 bilionth digit of
bilionth digit of 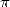 in base 2. The revolution had started.
in base 2. The revolution had started.
Plouffe
extend this result in all the bases 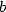 in octobre
1996 [22] to the
price of a time
in octobre
1996 [22] to the
price of a time 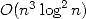 and the clever uses of the serie
and the clever uses of the serie
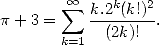 |
(19) |
Some improvement in 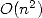 then
in
then
in 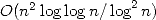 are
successively offered by Bellard in
1997 [5] then
Gourdon in 2003 [14].
Numerous other formulae of type BBP ( with powers of
are
successively offered by Bellard in
1997 [5] then
Gourdon in 2003 [14].
Numerous other formulae of type BBP ( with powers of  or
or 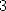 ) have since
then seen the day for the logarithm of integers,
) have since
then seen the day for the logarithm of integers, 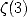 ,
, 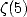 , the
Catalan's constant
, the
Catalan's constant 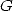 , and in general polylogarithm constants [9, 17].
Unfortunatly, there propably does not exist any formula for
, and in general polylogarithm constants [9, 17].
Unfortunatly, there propably does not exist any formula for 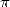 with a power
with a power 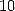 , in other
words in base
, in other
words in base 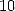 . The formula
. The formula 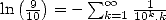 shows however we can calculate isolated decimal digits of certain
constants.
shows however we can calculate isolated decimal digits of certain
constants.
Those fundamental results shows in particular
that  belongs to the class of complexity of Steven
belongs to the class of complexity of Steven 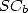 ,
regrouping the constants that we can calculate the digits in base
,
regrouping the constants that we can calculate the digits in base 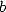 in polynomial
time and memory
in polynomial
time and memory 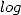 -polynomial, which was before judged to be improbable
from a memory point of view.
-polynomial, which was before judged to be improbable
from a memory point of view.
Since then, Fabrice Bellard,
a Polytechnician French studient, managed to reach the 1000 billionth
digit in septembre 1997. Then Colin Percival reached the 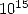 -th
binart digit of
-th
binart digit of 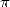 (a
(a  !) by a collaboratif calculation on the internet of 1.2
million hours of shared CPU between 1734 computers spread in 56
countries between the 5th septembre 1998 and the 11th september 2000!
!) by a collaboratif calculation on the internet of 1.2
million hours of shared CPU between 1734 computers spread in 56
countries between the 5th septembre 1998 and the 11th september 2000!
The principle of this calculation of the 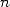 -th digit of
-th digit of 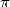 is given on
the page N-th
digit.
is given on
the page N-th
digit.
4.2 A formula full of resources
The nearly direct access of the digits of
those constants seeded the idea in mathematicians that we can find some
properties on the spread of those digits , and that we can be near a
proof for the normality of 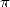 (and hence the irrationality of the Catalan's
constant
(and hence the irrationality of the Catalan's
constant 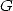 or the odd
or the odd 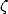 ). The normality of a number requires that each
). The normality of a number requires that each 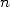 -uplet possible
appears with a probability
-uplet possible
appears with a probability 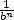 in the digits in base
in the digits in base 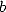 of this
number. For example each digits between
of this
number. For example each digits between  and
and 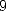 appear on
average once on
appear on
average once on 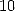 , each number between
, each number between  and
and  appears once
on
appears once
on 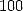 , and
so on. In octobre 2000, Bailey and
Crandall reduced this condition on normality to the satisfaction on the
following hypothesis
:
, and
so on. In octobre 2000, Bailey and
Crandall reduced this condition on normality to the satisfaction on the
following hypothesis
:
Conjecture 4.1 Let
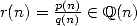 ,
, 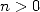 , with
, with 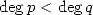 and
and  without poles on
without poles on 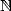 (its the polynomial
part of the BBP formulae). Let a base
(its the polynomial
part of the BBP formulae). Let a base 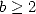 and
and 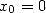 . The the sequence
. The the sequence
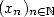 defined
by
defined
by
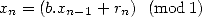 |
(20) |
has a finite attractor
or is equally spread on ![[0,1]](../histoire/histoire235x.gif) .
.
 |
|
|
| Richard E. Crandall |
|
|
| |
This kind of sequence is equivalent to the BBP
representation of a constant since if 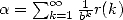 , then
, then 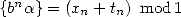 where
where 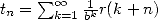 tends to 0
if
tends to 0
if 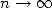 since
since  .
.
The condition of a finite attractor represent intuitively the fact that for a sequence of always approaching a set of finite value starting from a certain rang, and in any order, as we are tending it towards a genral rational (whose decimal sequence are periodic.
Definition 4.2 Precisly,
a sequence
![(xn)n (- N (- [0,1]](../histoire/histoire241x.gif) has a finite attractor
has a finite attractor  if
there exist
if
there exist  and such that for all
and such that for all  ,
,
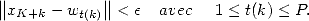 |
(21) |
We can furthermore show that in our case (BBP
formulae), this property is equivalent to the rationality of the limit
of 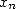 [4]. The notion of
evenly spreaded is more intuitive. It is checked if the proportion of
the appearation of a sequence of values in
[4]. The notion of
evenly spreaded is more intuitive. It is checked if the proportion of
the appearation of a sequence of values in ![[0,1]](../histoire/histoire248x.gif) in a given
interval
in a given
interval ![[c,d]](../histoire/histoire249x.gif) is exactly the length of that interval, basicly the
values taken are uniformly spread in
is exactly the length of that interval, basicly the
values taken are uniformly spread in ![[0,1]](../histoire/histoire250x.gif) .
. 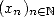 is
evenly spread if
is
evenly spread if
![lim Card-{xj (- -[c,d], j-<-n} = d- c.
n--> oo n](../histoire/histoire252x.gif) |
(22) |
The evenly spread for this kind of sequence
implies the normality [19].
Taking into account the various implied constants in the BBP
representation, we scratch here some important improvement, especially
for the odd 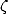 . It is amusing to see the simplicity of the BBP formula that leads to
all those consequences. Consult [4, 20]
to expand on those open questions.
. It is amusing to see the simplicity of the BBP formula that leads to
all those consequences. Consult [4, 20]
to expand on those open questions.
5 An endless quest ?
5.1 Record to date
The 6th december 2002. Kanada, untirable
competitor who holds or reclaim the record in the calculation of the
decimals of 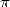 for more than 20 years, calculated 1 241 100 000 000 decimals of
for more than 20 years, calculated 1 241 100 000 000 decimals of 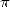 . The surprise
came from the fact that this time he only used two formula of the type Machin like equation 10.
. The surprise
came from the fact that this time he only used two formula of the type Machin like equation 10.
This comeback to suprisingly simple formulae after the use for fifteen years algorithms of Brent-Salamin, or Borwein or series of Ramanujan and Chudnovsky was really unexpected. It seems that the perpetual uses of roots, multiplications and divisions needed for the use of FFT was on a great scale. This last requires a lot of memory to function. Kanada hence went back to some wiser method like the formulae of type Machin, which sensibly needs more arithmetic operation but less FFT and hence a lot less memory. Kanada estimated that his implementation is roughly two time faster than the previous one he used, the algorithm 14 of Brent-Salamin and the one of quartic order by the Borwein (eq. 17). The calculations were done in hexadecimal base, i.e. 1 030 700 000 000 digits. The used formulae were :
The first was found in 1982 by a math profesor and composor, Takano, and the second was a discovery of Störmer in 1896.
This calculation by Kanada holds a second
suprise: since the result was obtained in base 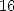 , after
checking the equality between the two calculation, he then did a second
check by directly calculating the 20 hexadecimal digits at the position
1 000 000 000 001 with the help of BBP formulae presented previously.
The result B4466E8D21 5388C4E014, which required 21 hours of work,
perfectly corresponded to the calculation done with the help of
, after
checking the equality between the two calculation, he then did a second
check by directly calculating the 20 hexadecimal digits at the position
1 000 000 000 001 with the help of BBP formulae presented previously.
The result B4466E8D21 5388C4E014, which required 21 hours of work,
perfectly corresponded to the calculation done with the help of 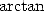 formulae.
The hexadecimals digits were then converted in base ten, a not so
trivial operation, reconverted into hexadecimals for verification, then
the record was official [2].
formulae.
The hexadecimals digits were then converted in base ten, a not so
trivial operation, reconverted into hexadecimals for verification, then
the record was official [2].
The calculations (everything included) lasted around 600 hours on a HITACHI SR8000/MP with 1TB of memory (1024GB), i.e. the same amount of memory as for its previous record of 1999, even though 6 times more decimals were calculated!
5.2 Perspective and motivation
How to explain that the race to the decimals
is still current news? The motivation to beat the record of decimals of
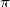 have
in fact never run out. We will mention mixed and mash the test of
computer (a bug was discovered by Bailey
during his record of the calculation in 1986 on a Cray-2), the hypothesis of irregular
appearance in the spread of calculated decimals (still nothing on that
side) or the addition of yet more efficient implementation of the
decimal calculation (the computation is running like a fever on the
internet between several mathematician programer for the title of the
fastest program in the world).
have
in fact never run out. We will mention mixed and mash the test of
computer (a bug was discovered by Bailey
during his record of the calculation in 1986 on a Cray-2), the hypothesis of irregular
appearance in the spread of calculated decimals (still nothing on that
side) or the addition of yet more efficient implementation of the
decimal calculation (the computation is running like a fever on the
internet between several mathematician programer for the title of the
fastest program in the world).
Each of these reason taken seperatly is not
sufficient. It would be more truthful to say that its the conjection of
all those reason, without taking into account the passion started by
the "personality" of 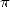 , which feeds and renew the competition. It is tru that
the mordern implementation of arithmetic libraries on large numbers
(based on the FFT , and Newton technics seen previously)
helped a lot in the race of decimals of
, which feeds and renew the competition. It is tru that
the mordern implementation of arithmetic libraries on large numbers
(based on the FFT , and Newton technics seen previously)
helped a lot in the race of decimals of 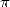 . It is also
true that putting together efficient program is not in everyone's reach
and that you need to carefully know the architecture of your calculator
to have any hope of an interesting performance. It's a challange for
numerous computer scientist gifted in maths (or the other way round!).
We have also seen that the recent discovery of the BBP formula 18 opened up a
large field of theoretical investigation.
. It is also
true that putting together efficient program is not in everyone's reach
and that you need to carefully know the architecture of your calculator
to have any hope of an interesting performance. It's a challange for
numerous computer scientist gifted in maths (or the other way round!).
We have also seen that the recent discovery of the BBP formula 18 opened up a
large field of theoretical investigation.
I will add that the popalarity of 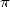 plays an
important role: it is this justification that is maybe rarely mentioned
but which is taken in full with simple amators of matheamticians member
of the lovers of
plays an
important role: it is this justification that is maybe rarely mentioned
but which is taken in full with simple amators of matheamticians member
of the lovers of 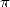 sects, or even visible by sifting through maths forums
over the worlds: the theory of numbers, classical analysis and the
constants have an accesible base, at least in appearance, for the
non-mathematicians and stay the greatest giver of little excersices of
some funny properties of numbers. Its through this bias that is born
many vocations of mathematics, and we just need to consult
mathematicians web pages like Bailey, Plouffe ,
Kanada or the Borwein brothers to be
convinced that they keep at over fifty years a refreshing passion for
the constants, visible part of the math iceberg. The difficulty of
abstraction of other mathematics domains like algebraic geometry
confines them more to a more knowledgeable audience and they do not
benifits from as many nearly universal symbols like
sects, or even visible by sifting through maths forums
over the worlds: the theory of numbers, classical analysis and the
constants have an accesible base, at least in appearance, for the
non-mathematicians and stay the greatest giver of little excersices of
some funny properties of numbers. Its through this bias that is born
many vocations of mathematics, and we just need to consult
mathematicians web pages like Bailey, Plouffe ,
Kanada or the Borwein brothers to be
convinced that they keep at over fifty years a refreshing passion for
the constants, visible part of the math iceberg. The difficulty of
abstraction of other mathematics domains like algebraic geometry
confines them more to a more knowledgeable audience and they do not
benifits from as many nearly universal symbols like 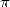 or the prime
numbers can be in number theory. We can compare hence the quest of
decimals of
or the prime
numbers can be in number theory. We can compare hence the quest of
decimals of 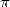 with the one of the greatest Mersenne prime for example, excersice much
in fashion at the moment (on the day I wrote this text, the record has
fallen again with the 43rd known Mersenne prime
!).
with the one of the greatest Mersenne prime for example, excersice much
in fashion at the moment (on the day I wrote this text, the record has
fallen again with the 43rd known Mersenne prime
!).
But I should propably give the last word to
Genuys to whom we asked, after his record of 10000 decimales in 1958,
why he chosed 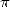 and who simply replied "It was for me a programing
excersice, I could have chosen an other number but
and who simply replied "It was for me a programing
excersice, I could have chosen an other number but  was too easy
and
was too easy
and  (Euler's constant) too hard! Plus there was the record!” [21].
(Euler's constant) too hard! Plus there was the record!” [21].
 |
|
|
| François Genuys in 2004 |
|
|
| |
References
[1] J. Arndt, C. Haenel, ”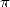 Unleashed”,
Springer-Verlag, Berlin Heidelberg New York, 2001.
Unleashed”,
Springer-Verlag, Berlin Heidelberg New York, 2001.
[2] D. H. Bailey, “Some Background on Kanada’s Recent Pi Calculation”, may 2003, preprint, http://www.nersc.gov/~dhbailey/dhbpapers/dhb-kanada.pdf.
[3] D.H. Bailey, P.B. Borwein, S. Plouffe, “On the Rapid Computation of Various Polylogarithmic Constants”, Mathematics of Computation, 1997, vol. 66, pp. 903-913.
[4] D. H. Bailey, R. E. Crandall, "On the Random Character of Fundamental Constant Expansions", Experimental Mathematics, 2001, vol. 10, no. 2, pp. 175-190.
[5] F. Bellard, “Computation of the n’th digit of pi in
any base in 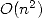 , unpublished, 1997,
http://fabrice.bellard.free.fr/pi/pi_n2.ps.
, unpublished, 1997,
http://fabrice.bellard.free.fr/pi/pi_n2.ps.
[6] L. Berggren, J. Borwein, P. Borwein, ”Pi : A Source Book”, Springer-Verlag, 2nd ed., 1997.
[7] J. Borwein, P. Borwein, “PI and the AGM: A Study in Analytic Number Theory and Computational Complexity”, Wiley, 1987.
[8] R. Brent, “Fast multiple-precision evaluation of elementary fonctions”, Journal of the Association of Computing Machinery, 1976, pp.242-251.
[9] D. J. Broadhurst, “Polylogarithmic ladders, hypergeometric series and the ten millionth digits of z(3) and z(5)”, 1998, preprint.
[10] S. A. Cook, S. O. Aanderaa, “On the minimum computation of functions”, Trans. AMS, 1969, vol. 142, pp291-314.
[11] J. W. Cooley, J. W. Tukey, “An algorithm for the machine calculation of complex Fourier series”, Math. Comp. 1965, vol 19, pp. 297-301.
[12] J.-P. Delahaye, ”Le Fascinant Nombre  ”,
Bibliothèque Pour La Science, Belin, 1997.
”,
Bibliothèque Pour La Science, Belin, 1997.
[13] P. Eymard, J.-P. Lafon, ”Autour du Nombre  ”, Hermann,
Paris, 1999.
”, Hermann,
Paris, 1999.
[14] X. Gourdon, “Computation of the n-th decimal digit
of 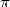 with
low memory”, preprint, 2003,
http://numbers.computation.free.fr/Constants/Algorithms/nthdecimaldigit.pdf.
with
low memory”, preprint, 2003,
http://numbers.computation.free.fr/Constants/Algorithms/nthdecimaldigit.pdf.
[15] X. Gourdon, P. Sebah, “N-th digit computation”, preprint, 2003, http://numbers.computation.free.fr/Constants/Algorithms/nthdigit.pdf.
[16] M. D. Householder, “The Numerical Treatment of a Single Nonlinear Equation”, 1970, MacGraw-Hill, New-York.
[17] G. Huvent, “Formules BBP”, 2001, Preprint.http://ano.univ-lille1.fr/seminaries/expo_huvent01.pdf.
[18] D. E. Knuth, “The Art of Computer Programming. Vol. 2: Seminumerical Algorithms”, Addison-Wesley, Reading, MA, 1981.
[19] L. Kuipers and H.Niederreiter, “Uniform distribution of sequences”, Wiley-Interscience, New York, 1974.
[20] J. C. Lagarias, “On the normalityof fundamental constants", Experiment. Math., 2001, vol. 10, no 2.
[21] “Le nombre 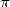 ”, Le Petit Archimède, Association pour
le Dévelopement de la Culture Scientifique, Amiens, 1980.
”, Le Petit Archimède, Association pour
le Dévelopement de la Culture Scientifique, Amiens, 1980.
[22] S. Plouffe, “On the computation of the  -th decimal
digit of various transcendental numbers”, unpublished, 11/1996.
-th decimal
digit of various transcendental numbers”, unpublished, 11/1996.
[23] E. Salamin, “Computation of 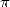 using
arithmetic-geometric mean”, Mathematics of computation, 1976, vol. 30,
pp. 565-570.
using
arithmetic-geometric mean”, Mathematics of computation, 1976, vol. 30,
pp. 565-570.
[24] A. Schönhage, V. Strassen, “Schennelle Multiplikation grosser Zahlen”, Computing, 1971, vol. 7, pp. 281-292.
[25] J. Tropfke, “Geschichte der Elementarmathematik”, Vierter Band, Ebene Geometrie, Dritte Auflage, Walter De Gruyter & Co, 1940.
back to home page