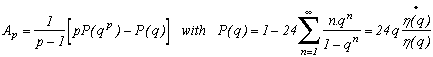Slices of life

Jonathan and Peter Borwein are Canadian mathematicians being a part of the CECM connected with the university Simon Fraser of Vancouver.
Jonathan is the director and his brother Peter is the associated director. For more information, click their names and you will go on their personal page.

About

For more than 15 years, these two revolutionized research on Pi! After the algorithm with quadratic convergence found by Brent/Salamin in 1976, they practically then monopolized the discoveries of series. Quadratic, cubic, quadric, nonic the speed of convergence did not stop since!
In fact, they proved some years ago, that an algorithm with speed n-ic converging Pi exists for every integer n... But the complexity of calculations increase very fast and it seems that the algorithm with quadric convergence represents the best ratio complexity/speed... It was moreover used in most of records since its discovery and notably by Kanada to calculate 51 billions of decimal recently.
You will have understood it, Borwein represents with the small group composed of Chudnovsky, Simon Plouffe, Garvan, Gosper et Bailey, the highlight of the active research on Pi today.

As regards the proof of these formulae, I must regrettably pass besides the great principle of this site... Because these proofs are already transcribed on Web at the following address: www.cecm.sfu.ca/organics/papers/garvan/paper/html/paper.html. It is necessary to recognize also that it would be useless to copy out silly 4 or 5 summaries of demonstration without being able to complete the intermediaries of calculation (even though principle is rather simple to understand), because not being of the level of a mathematician...

I retranscribe so only the summary of the proof for the 3) (2-nd formula), which is perfectly representative of the principle of demonstrations using modular equations (to see the page dedicated to Ramanujan for the explanation of this theorie and of the principle of the démonstration)

Proof

The techniques of this proof mainly appeal to theta functions, to the Eta function of Dedekind and to their properties.

1.1 Introduction :

So let us put Thêta functions:
, r>0

Then, function from the Borwein is introduced : rR^+*,

When r->+, q -> 0 and .

We are going to build an infinity of series _p and find a relation between _p(N²r) and _p(r) (As the Borwein say, it is a "nice" relation if N=p !)

2.1 Construction of series _p

For it, we pose q=exp(2i) and function of Dedekind is considered :

We remind the relation found by Euler :

2.2 This Eta function admits as property, among further :

2.3 Let us put besides :


2.4 And let us put finally (yeah!) _p function defined by :

(Easy to remember, of course...)

2.5 We have :

A_p(r)=1+O(q)

2.6 and according to 2.2,
We have then
(All these previous relations are very difficult to find but fortunately true (!) and principle is interesting)

2.7 So for r=1 we have (Does not depend of !!)
2.8 Besides we have, as well as for :
3.1 Relation between _p(N²r) and _p(r)

Let N, p1, we obtain :


Exceptional relation on which are based all these algorithms!!

3.2 According to 2.4, we have :


(Used series is called the series of Eisenstein E₂(q))

3.3 According to 3.1, we still have :


3.4 And so for N=p we have according to 3.1 :

Now according to 3.1 and 2.6 we have :

m_p,p()=p

3.5 So we find for r= and according to 2.6 :

_p()=

(Well, would not it be a good point of departure for =0,318... !!)

4.1 Construction of the algorithm

We put

_n=_p(r₀ p²ⁿ)

r₀ p²ⁿ -> + when n -> +
so _n ~ because _p(r₀ p²ⁿ) -> according to 2.8.
We also put

m_n=m_p,p(r₀ p²ⁿ)

This writing not being what we can call the most practical, so we are going to find a relation between _n and _n-1 knowing that :
₀=_p(r₀) for r₀=, so ₀=.

The first part of the general study is ended. To build the algorithms, the series consists in choosing one singular p and then to introduce modular forms a(q), b(q) and c(q). The existence of a relation between a(q), b(q), c(q) and a(q^P ), b (q^P ), c(q^P) supplies modular equation

a ^p+b ^p=c ^p

(No, no, it is not Last Fermat's theorem !!)

By defining :
, we have s^p+(s*) ^p=1 and relations between s, s* and supply the algorithm...

Application to the order 2 (p=2) :

5.1 Definitions :

According to 3.2, we have A₂(q)=2P(q²)-P(q)=₃⁴(q)+₂⁴(q) according to 1.1 and 3.2

Let us put besides :

5.2 a(q)=₃⁴(q)+₂⁴(q)
5.3 b(q)=₄⁴(q)
5.4 c(q)=2₂²(q)₃²(q)

Associated modular equation is :

5.5 a²=b²+c²

With 3.1 we have :

5.6
Then according to 5.2 à 5.5, we find (not easily) :

5.7 and
5.8 a(q)=a(q²)+3c(q²)

By posing s and s* as defined higher, we deduct from it :
5.9 and
5.10 , good...

We have with 5.5 :
5.11 s²+(s*)²=1

According to 5.9 and 5.6, we have :
5.12 m_2,2(r)=(1+3s(q²)) (not too difficult, that!)

And, with 5.10 and 5.9

On the other hand, according to 3.4 and 5.12, we have


5.13
Now, of 3.4 and 3.5, we know that ₂()= and m_2,2()=p=2
and according to 5.12, 2=1+3S(2) so S(2)=.
5.14 One has then _n=(4ⁿ)
5.15 and s_n=S(4ⁿ)
So, finally, we have ₀=, s₁=S(2)=, and

and with 5.13,

_n=(1+3s_n)_n-1 - 2^n-1s_n

Where from we obtain (finally!) the algorithm :

That is the most frustrating in this proof, it is the simplicity of the principle and the parallel horror of the calculations that does not appear here because the most difficult results are admitted...


Concerning series, I have the general formula of forming these series and the principle, but not having understood everything, I let you to go to watch the site of Borwein :



First series corresponds to the case t=427 and the second in the case t=1555.

Trials

No attempts found on the net, so, there here is. Obviously, they are quite amazing!
The second formula was tested also in the chapter Salamin...

For the following ones, let us cling! Order indicates the speed of convergence (2-> quadratic, 4-> quadric), and the figure in brackets formula to that test refers...

n=	1	2	3	4	5	6	7	8	9	10	12
Ordre 2 (2)	2	8	18	40	83	170	344	693	1392	2789
Ordre 2 (3.2)	0	2	7	18	40	84	171	345	694
Ordre 4	7	40	170	694							29360128
Ordre 5	5	31	166	848

I was not able to test upper orders in 5, my exceeding current computer 100 decimal of preciseness (that is pitifully small, on looking at the speed of the convergence!)