Lord William Brounker
(1620 - 1684)

Important formula

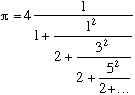
Other continued fractions...

Reference from the Encyclopedie of Integer Sequences : A001203

Slices of life

Doctor in linguistic and philosophy in 1647 in Oxford and founder with Wallis of Royal Society, William Brounker likes nevertheless mathematics. At request of his friend Wallis, he begins researches on and continuous fractions, that allows him to propose the development of /4 under this form according to Wallis' formula.

About

There are other numerous continued fractions calling out . Regrettably, their convergence is not very fast, they are unusable in practice, but it suggest another way to represent the numbers instead of classic decimals. According to some, Ramanujan had maybe the gift to think the numbers in term of continuous fractions, that would explain partially its surprising results...

Proof

A little of theory about the continuous fractions which disappeared totally of education! The reduced fraction of a generalized continuous fraction is written: .
we can calculate the reduced P_n and Q_n by the formulae of recurrence :
P_n+1=b_n+1P_n+a_n+1P_n-1 and Q_n+1=b_n+1 Q_n+a_n+1 Q_n-1 (noted (1) and (2)).
We have in our case a₀=0, a₁=1, a_n=(2n-3)² for n>1, b₀=1, b_n=1 for n>1.
Another very useful formula is P_nQ_n-Q_nP_n-1=(-1)ⁿa₁.a₂.....a_n (3)
And finally, fraction converges or not at the same time as series
a₀+ (4) and has even limit in case of convergence.
Check, let us spend in the practice and let us apply these formulae to the fraction of Lord Brounker... Let us show by recurrence, (it is the most painful!) that proposition A_n : Q_nQ_n-1= (H1) and =(2n-1) (H2) is true for every n>2.
No problems for n=2 because and Q₂ Q₁=3.
Later, it is a little heavier... Let us suppose result for some n> 2.
We have according to (2) Q_n+1Q_n=2Q_n²+(2n-1)²Q_n-1=2Q_nQ_n-1+(2n-1)²=(2+(2n+1)²)=(2n+1)(2n-1) d'après (H2)
=and it is well (H1) in the following rank which will be noted moreover (H3).
On the other hand, according to (H1), (H2), and (H3)
So finally, =(2n+1) that is well (H2) in the following rank. The theorem of recurrence allows us to conclude with the validity of A_n for n>2.
And with (4) and the convergence of the series according to Leibniz, we conclude that is well the value of the continuous fraction proposed by Lord Brounker...

Trials

Regrettably, if the formula is beautiful, the fact that reduced fraction converges as the series of Leibniz implies execrable results. Because results are the same, refer to Leibniz for the detail of attempts...

Other continued fractions (quite so beautiful!!)