Blazon of the Polytechnic school

Fabrice Bellard
(1973)

avec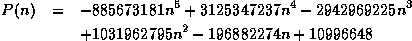

Slices of life

Fabrice Bellard is a rather exceptional boy. Maybe one of the brightest of our generation. After brilliant studies in the secondary school and in preparatory classes at Joffre ( Montpelier) where, he already conceives a software of compression of data without loss ( the famous LZEXE), he enters the Polytechnique school (76-th in the competition on 6000 candidates) in 1993. He has choosen then Télécom Paris as school of specialization in 1996.
Designer of numerous software packages in domains as varied as compression, 3D, music, it is certainly an information scientist of very first plan!
An only 36 years old, his professional experience and its realizations are yet impressive as we can see on his site.

About

After some calculations in 1995, Fabrice Bellard was interested more and more in Pi and notably discovered the two formulae above. Let us note nevertheless that the second one is not demonstrated...

Furthermore, Simon Plouffe elaborated an algorithm in 1996 to calculate in decimal system (and either in hexadecimal system as the formula BBP) the nth digit of Pi. Regrettably, the complexity in O(n³Log(n)) made it unusable in practice. Well, Bellard simply made changes and improved the algorithm in O(n²)! That's something!

But his great blow of brightness is the calculation in binary of 1000 billionth digit of Pi (which is one 1 by the way!) using several stations of Ultrasparcs...

Current record is 40 000 billionth digit in binary of Pi (0) by Colin Percival.

Proof

Well here is the summary of the demonstration such as Fabrice Bellard gives it. For the second formula, I found a proof, see the page Hypergeometrics.

We consider with z<1

So in particular:
(1)
(2)
If we make a=2 in (1), we obtain :

It is enough then to consider relations in Arctan :

And with the relation ( 3 and 1 ), we obtain :


that, with reorganization of terms, allows to obtain the final formula down from the page...

Trials

Here we go! This formula improves in theory of 43 % calculation with the formula BBP. The form indicates to us that convergence is in 10.n.log(2)=3n about, what is well!

n=0	3,1417
n=2	9 decimals right
n=5	19 decimals
n=10	34 decimals
n=20	64 decimals

And for the second formula :

n=1	0,02452 !!
n=5	3,1416
n=10	12 décimales
n=20	32 décimales
n=50	94 décimales

Well here is a convergence which accelerates! At least in the beginning because over the first values of n, it is going to stabilize. By applying the equivalence of Stirling to the term of the series, we find moreover that the speed of convergence is 2,12.n-5.log(n) about there, that is all the same rather correct.