|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|

Finding the 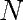 th digit of a number a without needing to know the
previous one thanks to the BBP formula
th digit of a number a without needing to know the
previous one thanks to the BBP formula
1 The BBP formula
Little reminder: On the 19 septembre 1995 at 0h29 (!), after month on research in the dark, Simon Plouffe, David Bailey and Peter Borwein de Vancouver discover the apperently simple and innocent formula
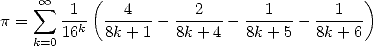 |
(1) |
now called the BBP formula (see Plouffe's page). Our three canadians noticed
that this expression is very close to a decomposition in base 16 of 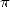 . In the 1996 article [1]
that is now famous, they show that you can use 1
to find the
. In the 1996 article [1]
that is now famous, they show that you can use 1
to find the 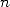 th digit of
th digit of 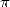 in base
in base 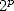 (all the more in base 16)
without having worked out the previous digist, all of this in roughly a
linear time
(all the more in base 16)
without having worked out the previous digist, all of this in roughly a
linear time 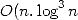 ) and in space
) and in space 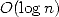 !!
The space required being so small, they apply straight away this result
by calculating the
!!
The space required being so small, they apply straight away this result
by calculating the 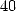 billionth digit of
billionth digit of 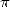 in base 2.
in base 2.
Let's stop now working on the calculation of
the 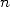 th digit of
th digit of 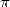 by considering the general case of a number
by considering the general case of a number  and an associated BBP formula:
and an associated BBP formula:
2
Finding the 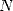 -th digit of a number
-th digit of a number  without knowing the previous one
without knowing the previous one
We will follow here, with a few adaption, the
very clear explenation of Xavier Gourdon and Pascal
Sebah on the subject [2]
which already simplified the original article [1]. X. Gourdon knows a lot on claculation
algorithm since he is the current holder (for quite a few years) of the
speed record in calculating the decimals of 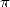 with the program PiFast (even
faster than the program made by Kanada's team).
with the program PiFast (even
faster than the program made by Kanada's team).
To simplify the reasoning, we will restrain
ourself to base  , and the
, and the 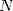 th bit of
th bit of  defines the
defines the 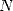 th bit of the fraction part of
th bit of the fraction part of  , that is the part after the dot. The fraction part of a
number shall be written as
, that is the part after the dot. The fraction part of a
number shall be written as ![{x}= x- [x]](../mathematiciens/nieme_digit/nieme_digit25x.gif) .
.
2.1 Shift
The first idea relies on the following theorem
Theorem 2.1 The
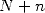 th bit of
th bit of  is obtained by calculating the
is obtained by calculating the
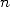 th
bit of
th
bit of 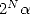 i.e. the
i.e. the 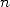 th
bit of
th
bit of 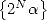 .
.
Proof. Decomposing
 in base
in base 
![a = [a]+ {a}= sum ak+ sum ak, (a (- {0,1})
2k 2k k
k<0 k>0](../mathematiciens/nieme_digit/nieme_digit34x.gif) |
(2) |
where  . The
. The  th bit of
th bit of  is therefore
is therefore 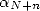 which as wanted is the
which as wanted is the 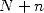 th bit of
th bit of  . __
. __
Example 2.2 Let's
find the 13th bit of  . Since we have
. Since we have 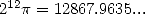 , in
particular,
, in
particular, 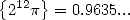 .
All that is left now is to work out the
.
All that is left now is to work out the
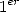 bit of
bit of 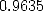 . Changing into binary, we get
. Changing into binary, we get
![-1 1- -1 1- 0- -1 1-
0.9635...= 21 + 22 + 23 + 24 + 25 + 26 + 27 + ...= [0.1111011...]base 2](../mathematiciens/nieme_digit/nieme_digit46x.gif) |
(3) |
hence the 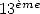 bit of
bit of 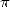 is
is 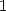 , and the
, and the 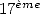 bit is
bit is  .
.
Finding the 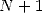 th bit of
th bit of 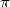 is therefore the same as finding the first bit of
is therefore the same as finding the first bit of 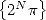 . Using the BBP formula 1,
this correspond to the first bit of the serie
. Using the BBP formula 1,
this correspond to the first bit of the serie
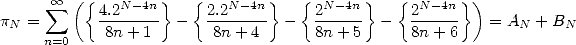 |
(4) |
where 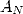 and
and 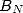 are the sums
are the sums
 |
(5) |
Taking into account the fast decrease of 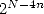 for
for 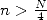 , we just need to evaluate the first
few terms of
, we just need to evaluate the first
few terms of 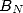 (in floating point form!), plus exacly enough
for the rest of the sum is less than the presicion needed (here
(in floating point form!), plus exacly enough
for the rest of the sum is less than the presicion needed (here 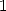 bit after the dot).
bit after the dot).
Concerning 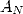 , we can put its general term in the form
, we can put its general term in the form
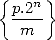 |
(6) |
with 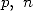 and
and 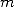 in
in 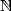 . By writting
. By writting 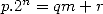 the euclidien division of
the euclidien division of 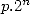 by
by 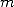 , we can see that
, we can see that 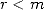 ,
, 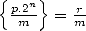 . This can also be
written as
. This can also be
written as
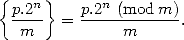 |
(7) |
2.2 Exponentiation
Imagine that we want to calculate the 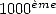 bit of
bit of 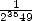 . Thanks to the previous principles,
this comes down to calculate the
. Thanks to the previous principles,
this comes down to calculate the 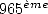 bit of
bit of 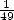 and so the
and so the 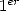 bit of
bit of 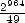 . Using 7,
we need to find
. Using 7,
we need to find  such that
such that 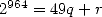 hence evaluate
hence evaluate 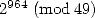 .
.
Calculating 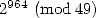 is done by a method called binary
exponentiation (or binary powering), whose idea seems to have been
already used before 200 BC [3],
and even considered by the Egyptians to carry out multiplication! This
simply comes down to using modulo
is done by a method called binary
exponentiation (or binary powering), whose idea seems to have been
already used before 200 BC [3],
and even considered by the Egyptians to carry out multiplication! This
simply comes down to using modulo 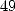 arithmetic, in other words working in
arithmetic, in other words working in 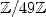 , in three steps
:
, in three steps
:
- We decompose
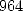 in powers of
in powers of  :
: 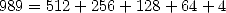
- We calculate each steps the
power of untill we reach
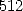 :
: 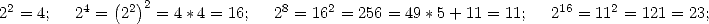
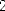
- We use step 1 et 2 :
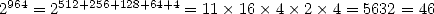 .
.
More generally to obtain 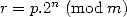 , we set
, we set  to 1 and we take the biggest power of
to 1 and we take the biggest power of  less than
less than 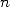 . Then we apply the following algorithm that is
equivalent to our example
:
. Then we apply the following algorithm that is
equivalent to our example
:
Finnaly we end up with 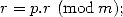 to take into account
to take into account 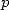 . Due to the decomposition of
. Due to the decomposition of 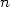 in
powers of
in
powers of  , we use
, we use  operations for this
calculation, which is very weak
!
operations for this
calculation, which is very weak
!
2.3
Final Steps
All that is left is to obtain 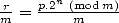 and then to sum
evrything on
and then to sum
evrything on 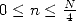 to obtain
to obtain 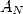 in 5.
We need to note that if the calculation of every term of
in 5.
We need to note that if the calculation of every term of 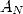 is done in floating point form and that, say, the last
bit is wrong, then in the worst case scenario the of the remainders on
the whole sum will produce an error on
is done in floating point form and that, say, the last
bit is wrong, then in the worst case scenario the of the remainders on
the whole sum will produce an error on 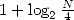 bits. For the values of
bits. For the values of 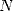 non-excessive, we can in all calmness carry out the
calculations of
non-excessive, we can in all calmness carry out the
calculations of 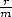 with an arithmetic precision of only
with an arithmetic precision of only 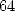 bits.
bits.
For this reason and by noting that for 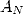 , we sum
, we sum 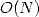 termes each needing
termes each needing 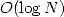 operations due to the exponentiation, the algorithm
requires
operations due to the exponentiation, the algorithm
requires 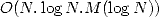 operations and
operations and 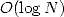 in space, where
in space, where 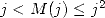 is the complexity of the
multiplication of two integers of size
is the complexity of the
multiplication of two integers of size 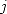 bits.
bits.
References
[1] D.H. Bailey, P.B. Borwein, S. Plouffe, “On the Rapid Computation of Various Polylogarithmic Constants”, Mathematics of Computation, 1997, vol. 66, pp. 903-913.
[2] X. Gourdon, P. Sebah, “N-th digit computation”, preprint, 2003, http://numbers.computation.free.fr/Constants/Algorithms/nthdigit.pdf.
[3] D. E. Knuth, “The Art of Computer Programming. Vol. 2: Seminumerical Algorithms”, Addison-Wesley, Reading, MA, 1981.
back to home page

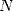 th digit of a number
th digit of a number  without knowing the previous one
without knowing the previous one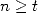 , Then
, Then 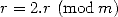 ;
; 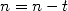 ; EndIf
; EndIf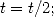
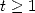 Then
Then 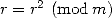 ; Go to step 1.
; EnfIf.
; Go to step 1.
; EnfIf.