William Gosper

We have a general formula for x less than 1:

where ₂F₁ is a hypergeometric seie, which distract us from our topic, so I won't mention it....
For x=1/2, we get :
which has a convergence of 2n
For we can write :
of convergence 3.39n

William Gosper is also used to formulae that are a bit weird making use of , donc ask me of their use!
For example :






and by generalising :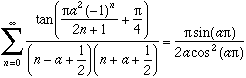

Slice of life

William Gosper is part of those passionate about Pi and of the small irreducible group that make computers suffer! Gosper had in fact already calculated 17,001,303 terms of the continue fraction of Pi in 1977. And then he programmed Ramanujan's serie (the one with 1103) to obtain 17 millions decimals. We did not know then if this serie converged, but the calculation was correct and only the number 1103 was not justified. So, as the Borwein said, the same as two different integers whose difference is less than one must be equal, the number 1103 was found to satisfy. Because all other numbers leads on decimals completly wrong dues to the sensitivity of errors...
Ah yes, still today, we have sometime to be contented with empirical proofs!
Nevertheless let us not take away the scientifical force of William Gosper, working on artificial intelligence, and on a small paquet of properties concerning factorial series converging to Pi with R. Schroeppel. Unfortunatly I don't have the proof for the one above, but it must be very similar to the proof below.
I don't if it is him and Schroeppel which found :

=

which seems to me a bit funny taking into account the relative simplicity of the serie and the proof!

Around

First of all, notice that the factorial serie at the top of the page will be perfecct for a spigot algorithm giving Pi, something that I will developpe later on, on a new page.
But since we are talking of a factorial specialist, let's use this opportunity to look at the other factorial series buzzing around Pi !
Note that for more simplicity...
So we get :



The formula (1) comes from the great Euler while that (2) comes from Comtet in 1974.
The similarity between those two sum with the sum of power inverses is quite stunning...



And of course, there exists no result for odd powers!

Proof

The proof for factorial series is a simple and same method, typical of freshers, that I give briefly here for the case of the formula :
=. By the way it's the same procedure that I used to rediscover the proof of Katahiro's formula...

If we consider .
This power serie has a convergence radius of 4. If we denote
hence the result is immediat by Alembert's criteria.

Since it's a power serie we can derive without any problem, and se we have:


The solving of the differential equation is just procedure, so I won't write it's details.... We get the following general and particular solutions:


We can deduce from the first result .

The we differentiate f and we get :


which ends the proof...

Hence, to get the general formula :
, we could notice that the members of the right and left hand side of the first equality satisfy the differential equation:

(1-x²)f'(x)-xf(x)=1 for x<1

Trials

All those sequences have linear convergence or very close to it (like a.n+b.Ln(n)) because the term in the serie decreases in c^-n.
Let's check this !

	Gosper sequence	Sequence from the proof	Sequence (2) Comtet
n=5	3,14159249 (6)	3,1306 (1)	3,1415911 (5)
n=10	12 correct decimals	3,14157 (4)	3,14159265340 (9)
n=50	57 correct decimals	28 correct decimals	35 correct decimals
n=100	?	58 correct decimals	66 correct decimals

Pretty conclusive, no?
Gosper sequence has a convergence of roughly 1,2n, which is quite good for this kind of sequence !
The sequence from the proof has 0,58n and the sequence of Comtet (2) has 0,66n.

Acceleration of the convergence

As always with sequence with linear convergence, the Delta2 by Aitken proofs to be useful, but a bit less than what one could hope for.

	Suite de Gosper	Suite de la démo	Suite (2) Comtet
n=5	3,1415926507 (8)	3,14195 (3)	3,1415924 (6)
n=10	14 correct decimals	3,14159277 (6)	11 correct decimals
n=50	61 correct decimals	31 correct decimals	38 correct decimals
n=100	?	62 correct decimals	69 correct decimals

3-4 extra decimals, which is not great, so we need to be content with pushing the series one or two extra strps no more!