Isaac Newton
(1642 - 1727)

(1) (2)


A similar sequence :

(3)

Slices of his life

Isaac Newton was born on Christmas day 1642. From a humble familly, he quickly became very inventive in his childhood. Entering the University of Cambridge in 1660, he met a profesor and friend who will become inportant during his formation, Isaac Barrow.
Newton quickly mastered the mathematics of his time. But the Great Plague (1665-1666) force him to go back to his natal village of Woolsthorpe, which give him some time for his mathematics and physics research.
And what research ! Law of motion (universal attraction), optical law are brilliantly tackled and Newton discover differential calculus (as simple as that) thanks to his method of fluxon (x+x^.o or x+dx in modern notation, well that is said that it was invented by his greatest rival Leibniz !)
Greatest rival because he and Newton would violently argue on the authorship on the invention of differential analysis that lasted till the end of their lives. The notations x^. or x¨ of Newton are still being used in physics...
The end of Newton the 20 march 1727 produced a scientifical mourning that has never been equaled in England. As a matter of fact he is buried at Westminster abbey.

Around

What interest us here, is of course and those two formula that followes from a clever analysis but which is un fact a particular case of the derivative of arcsin :

Proof

Let us proof the first formula in a "modern" and quick way so to leave space for the ingenuity of the original method by Newton for the second formula!

If we let y=Arcsin(x), that is x=sin(y) for -1<x<1, we easily get :
dx=cos(y)dy=(1-sin²(y))^1/2dy hence :

By a recurrence that I qualify as "nearly" straightforward, we change it:

Since it's a power serie with convergence radius of 1 (also straightforward from Alembert's criteria) we can integrate bewteen 0 and x on an open interval ]-1,1[ and we the get :

And here all fantasies are allowed !
We can replace x by anything, as long as -1<x<1...
  For x=1/2, we have :
which is the first formula !

Or we can choose



For the second formula, let us go back to the world of geometry :
Newton took a very original reasoning that we'll inscribe here:
Consider the circle of diameter AB=1 and OC=1/4 (hence =/3) :
Newton then looked to calculate the area of the region in bold ACD (Denoted a(ACD), a complete personal notation)

1. First, =/3 hence 6a(AOD)=R²=/4 since R=1/2
Wherer a(AOD)=/24 but ,


2. Secondly, Newton considered that a(ACD) is equal to the area swiped by the segment [MN] between the point A and the segment [CD],which can easily be seen !!
But by pathagorus AN²+NB²=AB² but AN²=AM²+MN² and NB²=MB²+MN²
Hence AM²+MN²+MB²+MN²=AB²
and so we then get 2MN²=AB²-AM²-MB²=1-x²-(1-x)²=2x(1-x)
We can then conclude that :

Since we are dealing with a power serie, we are perfectly allowed to integrate term by term. So we find :


Great, no ?

By taking into account the equation of the quarter circle (1-x²)^1/2 for x varing between 0 and 1, we similarly get :

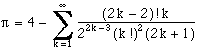
Trials

Those sequence have a nearly linear convergence that can be noticed just by looking at them... So the trials are by default not that interesting!

n=...	Sequence 1	Sequence 2	Sequence 3
5	3,1415767 (4)	3,1415950 (5)	3,170 (1)
10	3,141592646 (7)	3,1415926541 (8)	3,15256 (1)
50	33 correct decimals	34 correct decimals	3,1426 (2)
100	63 correct decimals	65 correct decimals	3,141965 (3)

The two first are what we expected with respecctive convergence of roughly 0,63n and 0,65n (the logarithm sums are neglible !). On the other hand, sequence 3 is very disapointing. Well, let's see why....

  Stirling's Equivalence gives us:




Which confirms the extreme slowness of sequence 3 (logarithmic convergence) and the relative speed of sequence 1 and 2 (linear convergence!). Furthermore, Log(4)=0,60... which also comply with the observations !
So be warn about series in factorial, a few can have a logarithm convergence if the denominator is more poweful in the equivalent term of the serie..... Luckely this is rare....

Note that the Delta2 of Aitken is practically useless in this kind of sequence (we only gain one decimal maximum for n100). This is not worth it... So, no chapter "Acceleration of the convergence"!