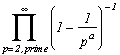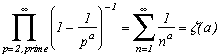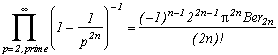Leonhard Euler
(1707 - 1783)

1) 1739
and more generally, we have
where Ber_2i is the Bernoulli's number with index 2i

(see appendix: Numbers of Bernoulli)

2)


3) et 4) (1737)

Slices of life

On looking at his quite complete scientific production, Euler was prolific concerning his formulae about .
Leonhard Euler was born at Basel in 1707. Son and grandson of a shepherd, Euler and his family are poor. His learning does not include mathematics, that induces him to take mathematic lessons with a student. At 13 years old, he begins studies of theology and philosophy of which he is awarded a diploma at 16 years old. His father intends him to become a shepherd, he gets ready for it but continues to study mathematics. His talent is noticed by Jean Bernoulli, a member of the great lineage of mathematicians of the same name, and in 1727, it leaves at the academy of the Sciences of St-Petersburg. The departure of Daniel Bernoulli from Russia allows him to become a professor of mathematics. He meets then the girl of a Russian artisan who gives him 13 children. Euler has a remarkable patience with his offspring and remained famous for his capacity to play while drawing up an article. He loses an eye after a rough fever.
Installed briefly at court of Berlin due to the invitation of Frédéric Le Grand, this one prefers nevertheless brilliant spirits as Voltaire, and treats him " mathematical Cyclops " (!). Returned in Russia, he becomes almost blind from 1771... He dictates nevertheless to his son his publications. He dies in St-Petersburg in 1783 by drinking some tea with his friends!

About

His production is huge... His works allowed the development of the analysis thanks to differential equations and integrals. he also approached differential geometry, the theory of the numbers and different fields of physics. Those that have worked with Euler considered him as the greatest mathematician of all the times! It is necessary to say that it published 800 pages of scientific text a year, all in all 75 volumes of 600 pages each! Indefatigable, he also imposed in a concern of perspicuity numerous notations as e (for the base of nepierian logarithms), i for the imaginary and (especially!) popularized notation (Introduced in 1706 by W. Jones).
His rigour is sometimes questionable but the ingenuity and the correctness of his results are remarkable! A good example is the way of which it found the result of the convergence of the sum of the squares inverses and that is told below:

Proof

For the mads about analysis!
But where to begin? Well, let us attend to the equality containing the numbers of Bernoulli, formula 1). Several demonstrations are possible, more or less complex... The one below presented, has the merit to be fast (everything is relative!) and is based on the first definition of the numbers of Bernoulli. it shows besides by completing the following demonstration of the formula 2) the equivalence of the two definitions of the numbers of Bernoulli...
Then just later, the original "demonstration" (hem!) due to Euler for the sum of squares inverses. If rigour is not really the first preoccupation, what an imagination and what a craftiness!
But that, it is for after the real proof...

---

1) We will be able to say indeed never enough thank you to Mister Fourier, its theory is going to be still very useful for us...

Considering the polynomials of Bernoulli B_2n(t), let us take a function f_2n for an integer n, of period 1, and that is equal to B_2n on [0,1 [. F_2n is obviously C¹ by fragments because restriction of polynomes in an interval of R. She verifies so the theorem of Dirichlet for T - periodic functions and one can write it like a series of Fourier.

1.1 First small intermediate result:

1.2 Let us calculate Fourier's coefficients now. Not to get bored pointlessly, let us show first of all by recurrence on n that B_2n is even with regard to x=1/2...
B₀=1 by immediate calculation so no problems for the rank 1...
Let us suppose for some integer n that B_2n(x+1/2)=B_2n(1/2-x)
Put g_2n+2(x)=B_2n+2(x+1/2)-B_2n+2(1/2-x). It is a polynôme so g_2n+2 is C² on R.
According to the hypothesis of recurrence...
So g '_2n+2 is constant now, g'_2n+2(0)=(2n+2)B_2n+1(0)-(2n+2)B_2n+1(0)=0 so g'_2n+2=0 so g_2n+2 is constant now g_2n+2(0)=0 and finally, B_2n+2 is very symmetric with regard to x=1/2, it is hypothesis in the following rank so proposition is valid for every integer n and on [0,1]. f_2n is symmetric with regards to x=1/2.
So the associated Fourier coefficient is obtained with b_k(f_2n)=
1.3 Let us calculate on the other hand for every integer n not nil
a_k(B_2n)=

= According to 1.1 then by immediate downward recurrence...
To there, everything is well! The rest is not much more complicated... We have indeed to calculate a_k(B₂).

1.4 One will be able to verify (because there is uniqueness) that B₂=X²-X+1/6 is well the Bernoulli's polynomial which is convenient for definitions. Then by simple double integration by parts, one has and . And naturally, , so, finally,
a_k(B₂)= .
1.5 One found so according to 1.3 and 1.4

a_k(B_2n)=

1.6 The development of B_2n In series of Fourier give us then for t in [0,1 [ :
and then specificly for t=0, one has:

where Ber_2n=B_2n(0)

And here is !

In view of the importance of the result, this demonstration is monstrously quick with regard to others ! And by patching a little, also two very useful expressions are obtained :

and

More generally, theses expressions are called Reynolds's sums :

So, for p=2n odd, we obtain the above sum, and for p even, one has:

with En the Euler's numbers that could be defined by :
or we can use the Taylor's developpement :
. We have in particular E_2n-1=0, E₀=1, E₂=-1, E₄=5, E₆=-61, E₈=1385

These numbers bring in Euler's polynomials of which I did not regrettably find definition. It is enough to apply the previous method to Euler's polynomials to find result.

Otherwise, with the first values of the numbers of Bernoulli and the first formula, one obtains:
Among others...

---

1) Encore... Here is the so original proof, of Euler himself, of the sum of invert squares... Convergence had been demonstrated by Jacques Bernoulli and Leibniz comes a cropper over, let us see what Euler made. He found the limit, but justifications are a little doubtful, you will see!

Basing itself on the theory of algebraic equations, Euler knew that the sum of invert roots of a_nxⁿ+a_n-1x^n-1+...+a₁x+1=0 worth -a₁. Considering then the development of It knows thanks to the periodicity of sine that the right member is nil for x=²,4²,9²,16²...
Euler says to himself whether the property is true for a finished polynôme it must be for an infinite polynôme and he deducts from it Is . Very strong !

---

2) Check, let us return in a little more serious things (mathematically!)... The demonstration of the general formula of the 2) (abbreviated, let us not misuse the calculation, and any more, I feel a little tired!) is on Fourier's page. An application z=1/2 gives :

.

But there is stronger! In one develops by exchanging sums (z inferior to 1 and absolute convergence of sums)

By posing t=2iZ and by calculating cotan by means of its expression in exponential complex (cos / sin), one obtains

=

According to the 2-nd definition of the numbers of Bernoulli. Oh oh!
By identification of terms two for two (it is two series), one can then end

!

It is effectively the good result shown in 1) and it is as well the original method that had used Euler. Here we are, 2 proofs for the price for one! It implies also the equivalence of the definitions of the numbers of Bernoulli (those of odd rank are indeed nil)

---

3) Ah, small break...

Well, let us move on the formula 3 now... Even there, Euler's monstrous craftiness intervenes... This one uses indeed a very unusual development, but o how effective, of arctan that is:

Arctan(t)=

For t positive... Euler used it with a formula of arctan =20Arctan (1/7) +8Arctan (3/79) to calculate 20 decimal of Pi in one hour (try so!). It is real that if one poses t=1/7, =0,02 ! Useful... Skillful, Euler was certainly...
Let us see indeed the demonstration:

3.1 Let us put x= x=, t positive and x in [0,1 [.
One has t=. Let us put y=Arctan(t)=Arctan

3.2 Let us try to simplify the writing... If z=Arctan, one obtains what gives sin²z=x and so

y=Arcsin.

But one does not see there always very clear... Let us continue so...
3.3 We derive this expression in x and one obtains :

2y'(x-x²)+y(1-2x)=1

3.4 Let us look there under the shape y=. Inserted into the differential equation, our eyes popping out of their sockets discover a₀+x(3a₁-2a₀)+=1+0.x+0.x²+... That, by identification, gives us a₀=1, 3a₁-2a₀=0 so a₁=2/3, and (2n+1)a_n-2na_n-1=0 so :

By immediate recurrence on integer n (hyper classic calculation!).
Mutually, one verifies that y= agrees how solution of the differential equation (not to forget, but do not count on me to make it!).

3.5 The rest is coarse as say some... According to the definition of y, we conclude for t positive real :

Arctan(t)=

But what can we make of it? Height of things! First of all apply described Euler's formula at the beginning of this section... May pose t=1 and obtain the formula 3) or t=1/2, or 1/4, or to use Arctan's formulae everything is possible! As usual, the more t is small, the more convergence is fast, because term in t in the sum is more and more small...
Me, I like t=, because we obtain so Arctan(t)=/6 :

That is very close to Schroeppel-Gosper's formula. Terrific!

---

4) Check, another proof... Even if I appear to be somebody which abbreviates more and more in the course of demonstrations, I can only give the tracks of the demonstration of the formula 4)... According to "Le fascinant nombre Pi" (see Ref.):
Is a> 1. For p prime number, p^a>1 so by limited development :

If these equalities for any prime number are written and that their product is made, one obtains to the left :

And to the right then? The product of right members is obtained, it is to say infinite sums. If one eliminates all the infinite products which are going to form (infinite products of terms in 1/p^ka give 0 would be it that because 0<1/p^ka<1/2), it stays the sum all the terms of the shape , are prime numbers and k, i, j complete... Does not it call back to you? Some theorem of arithmetic which says that quite complete n is decomposable under the shape p^kq ⁱr ^j... It is to say as product of prime numbers each to some power... As all the prime numbers and their powers are present here, one deducts from it that this infinite sum is worth :

And for has peer, one has then according to the formula 1) :

That is well the formula 4), if Pi is isolated!
These fabulous two equalities found by Euler will be reused in the page dedicated to Cèsaro. One of the important consequences of this result is that for a=1, the sum of invert diverges, so the product (left member) is worth infinity, so there is an infinity of prime numbers... Not bad, no? Here is that Pi makes a deafening entry to the world of the arithmetic!

Trials

Check, let us admit it, all these formulae are very beautiful but are not really made for the calculation of the decimal... The shape of the formulae of type 1) promises distressing one logarithmic convergence...

1)

n=10	3,0493 (0)
n=100	3,1320 (1)
n=1 000	3,1406 (2)
n=10 000	3,141497 (3)
n=1015	3,14159265358979228 (14)

A convergence about 0,434*ln (n)-1, driving to despair...
To note that I found on Internet (but I have no more address) a suite a little accelerating calculations:

But the dominant power of the being bottom 8, no miracles, this suite converges less fast than the following one :

n=10	3,1415926535860 (11)
n=100	19 decimals right
n=1 000	28 decimals right
n=10 000	37 decimals right
n=1010	92 decimals right

And a convergence about 4ln(n) +0,5, if that is not unfortunate!

2) Let us forget the formula 2) of the same kind that the 1) in a factor and a translation near, that does not change anything results...

3) The formula 3) turns out a little more interesting :

I take version t= in the development of arctan because, after all, it is faster than the formula 3)...

n=5	3,14131 (3)
n=10	3,14159244 (6)
n=50	30 decimals right
n=100	61 decimals right

Oh, a convergence shelf space about 3n/5, that is more friendly...

Hold, let us apply the formula of Machin with the development of Arctan found by Euler :

n=5	3,1415926500 (8)
n=10	15 decimals right
n=50	74 decimals right

A convergence shelf space of 3n/2, it is not bad at all!
And finally, let us apply the formula of arctan found by Euler to calculate the decimal of Pi:
=20Arctan (1/7) +8Arctan (3/79)

n=5	10 decimals right
n=12	21 decimals right
n=50	88 decimals right

7n/4 of convergence and one will notice that Euler had to calculate 12 iterations to obtain the decimal 20 of Pi... In 1 hour, it seems incredible! So tempt by hand!

4) To finish, the formula 4 has no calculus vocation and its shape lets expect from a logarithmic convergence, then...

Acceleration of the convergence

Any small paragraph, bus openly, nothing is terrible, even with Aitken's Delta2... But in slow convergence, presence of Delta2 certainly saves some suites of a pitiful flop...
For :

n=1000	3,14111 (3)
n=10000	3,141544 (4)
n=100000	3,1415921717 (6)

About log (n), not however badly, but all the same...
And for the formula of arctan with t= :

n=10	3,1415926520 (8)
n=50	34 decimals right

A convergence shelf space about 7n /10. Better, but not of what move mountains...