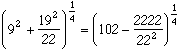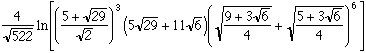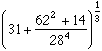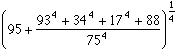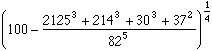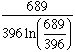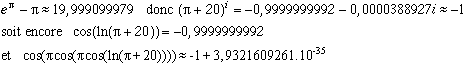Approximations and strange things about Pi

This page is devoted to the rational and irrational approximations which are nearest to Pi. And there are some great ones ! Not to mention some approximate curiosities concerning Pi.

Indeed, since people realised that there was a constant that defined the ratio of the perimeter of a circle over its diameter, a discovery dating from the Egyptians and the Babylonians, mathematicians have tried to give the exact value of Pi or, after the XVIIIth century, tried to give simple approximations of Pi.

 

During ancient times

Of course during antiquity mathematicians didn't know Pi was irrational, not even transcendant. So they believed some approximations of Pi were exact values ! This progression during antiquity is related on the geometric era page , I will just remind you of the values:

The Babylonians had estimated:

which was quite remarquable for that time.
The Egyptian scribe Ahmès had obtained :

=(16/9)²=3,16...

The Bible has remained famous for its hazardous approximation of : 3 !!

Let's not forget that Archimedes had set the limits of Pi, which showed that he was conscious of not being able to get the exact value.

In China, Tsu Chung Chih went ahead of the West, and suggested :

355/113 = 3,14159292...

But let's get back to the Western world. Still trying to get an exact value for Pi, Nicolas of Cues suggested :

The best of all was certainly Edward Johnston Goodwin (1828-1902) who in 1897 in Indiana (US), put forward a bill where several formulae, once applied, would have assigned to Pi the values 4 then 3.1604, then 3.2, and finally 3.232 ! Of course, this ingenious author had resolved the squaring of the circle, the trisection of an angle, and the duplication of the cube, which had been proved impossible a few years before, and he had allowed his discoveries to be used free of charge! Even the famous review American Mathematical Monthly, new at the time, had accepted two of his articles ! Fortunately, this project which was nearly accepted was finally refused because it was considered at the time that the law should not decide scientific truth... and a good job too!...

After the "renaissance"

The demonstration of the irrationality in 1761 then of the trascendence in 1882, destroyed howeverthe amateurs' and mathematicians' hope of getting the exact value of Pi, apart from the scatty man from Indiana. At that time, the fun was about to start, because people started to search for simple rational or irrational approximations of Pi . And the imagination and patience of mathematicians was fertile ! Check it out :


A few approximations :

Note from myself: Jean-Christophe Benoist noticed with pertinence that books about Pi (Delahaye, Warufsel...) used to sort the approximations of Pi as a function of the number of correct digits they provide. From this tenet, 3.14151 has a better rank than 3.1416 whereas the second approximation is the best. Moreover, two approximations having the same number of correct digits can't be discriminated.
He then proposed me to consider the score -Log₁₀(|approximation-Pi|) as a sorting criterion, which has the advantage of taking into account the real distance with Pi ! Thus, I included some values of this score for the smallest approximations into parenthesis.

Formulae	Approximated value	Correct digits of Pi
	3,1409	2 (3.21)
Kochansky's Approximation
	3,141533	4 (4.23)
Ramanujan's approximations
=	3,14164	3 (4.32)
	3,14182	3 (3.63)
	3,141623	3 (4.51)
	3,14164	3 (4.32)
	3,14159265258	8 (8.99)
	3,14159265258	8 (8.99)
	3,14159265380	9
	3,14159265358979432	14
	3,14159265358979265	14
	3,14159265358979312	15
	3,1415926535897932384190	19
	3,141592653589793238462642088	23
	3,141592653589793238462643383279	30
Castellanos' spproximations (1988)
(2e3+e8)1/7	3,14171	3 (3.91)
	3,141529	4 (4.20)
	3,141575	4 (4.76)
	3,14159704	5 (5.36)
	3,141592452	6 (6.70)
	3,14159259259	6 (7.21)
	3,141592649	7 (8.41)
	3,141592654111	8 (9.28)
	3,14159265363	9
	3,14159265358817	11
	3,14159265359037	10
	3,141592653589780419	13
Plouffe's approximations
437/23	3,1415398	4 (4.28)
	3,1415943	5 (5.77)
	3,14159267809	7 (7.61)
	3,14159259508	6 (7.23)
	3,14159265258	8 (8.99)
	3,14159265297	8
	3,141592653492	9
	3,1415926535949	10
	3,141592653586778	11
	3,1415926535912	10
	3,141592653589793238462649201	23
	3,1415926535897932384626433832797	30
Stoschek's approximation
	3,141104	3 (3.31)
And a few others
	3,141592920	6 (6.57)
=	3,1415333	4 (4.23)
103993/33102 (Euler)	3,14159265301	9

It is worth noting that Ramanujan (1913) and Olds (1963) gave a geometrical justification of the approximation 355/113. Gardner (1966) looked after . As for Dixon (1991) he was interested in and=.

---

Strange facts

All the above formulae are themselves curiosities because by inverting a formula giving Pi, you nearly get an integer or a rational or irrational fraction.
The best example is that of Roy Williams' expression with n a natural integer :
For certain values of n (particularly among Heegner's numbers 1,2,3,7,11,19,43,67 and 163), we almost find an integer :

n	Value of
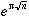
25	6635623,999341134233266067
37	199148647,999978046551856766
43	884736743,999777466034906661
58	24591257751,999999822213241469
67	147197952743,999998662454224506
74	545518122089,999174985664301733
148	39660184000219160,000966674358575246
163	262537412640768743,999999999999250072
232	604729957825300084759,999992171526856431
268	21667237292024856735768,000292038842412959
522	14871070263238043663567627879007,999848772648279480
652	68925893036109279891085639286943768,000000000163738644
719	3842614373539548891490294377805829192,999987249566012187

The "Fascinant nombre Pi" (see bibliography) tells us that Martin Gardner had used the case n=163 as an April fool's joke in 1975 saying that was an integer, which at the time was no easy to contradict ! In fact, this extraordinary particular case apparently comes from the fact that the algebric numbers field given by 163^1/2 has a unique factorisation proprety, as Heegner's numbers have particular arithmetic qualities.

Some precisions about this fact:
Ramanujan, (obviously !) had noticed that is close to an integer from less than 10^-12 which is really unexpected. His argument from the theory of modular functions was only understood dozens of years later.

This argument deals with the same function j as in the Borwein's page: we first consider (t complex number). This is a modular function, which means that it is defined on the superior complex half-plan, it has a limit in , it is meromorph and above all invariant under the transformation (a, b, c, d entiers).

Now, let's define an equivalence relation on the quadratic forms a.x²+b.xy+c.y² with a, b, c coprimes in Z (a>0). The discriminant is d=b²-4ac<0.

We define the relation ~ by a.x²+b.xy+c.y² ~ a'.x²+b'.xy+c'.y² if one form is the result of the other (and reciprocally) under the transformation :

This equivalence relation keeps intact the discriminant d. The number of equivalence classes is noted h(d) and a well-known theorem from Heegner (52), Baker et Stark (66) says that :

These integers are called Heegner's numbers.

Moreover, Webershowed that:

We then know that .

On the other side, being a meromorph function, j has a Laurent's development in q which is:

From the previous value , we get :

n being integer, which completes the proof.

The algebrical approach shows that Heegner's numbers are very important. The generated imaginary quadratic fields like have some fascinating factorization properties. For instance, the number of class of is 1 which is equivalent to the fact that the decomposition in prime factors in this field is unique.

Another curiosity is the number :



Less than 1 thousandth of an error with 20 for such a simple number, that's surprising isn't it?