|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|

Pi room in the "palais de la découverte" in Paris
For a fistful of digits ...
History of records and methods
Since Archimede, mathematicians tried hard to compute as many digits of Pi they could, even if it appears a useless quest to some people... But without this obsession, one must realize that we would have missed the recent discovery of several algorithms such as the product of long integers by fast fourier transform. And think about the consequences of the BBP formulas ! Thus, discover, optimize and accelerate the computation of the digits of Pi is a lively mathematical field.
Index table
Algorithms useful for computation of the digits of Pi
Computation records of Pi over the ages...
Digits computed by hand then using a computer
Place computed (digits in base 2 not knowing the previous ones)
Continued fraction of Pi
Digits record in a classroom
Pi memory records
World records announcements
About the world record of Takahashi-Kanada from april 1999 (68 719 470 000 digits)
About the world record of Kanada from september 1999 (206,158,430,000 digits)
About the world record of Kanada from december 2002 (1,241,100,000,000 digits)
A few statistics on Pi
1 000 000 digits of Pi
Algorithms useful for computation of the digits of Pi
- Aitken's Iterated Delta2 Process
A sequence transformation accomplishing an acceleration of convergence
- Newton Algorithm
- Reach the n-th digit of a number without knwoing the previous digits (Simon Plouffe's method)
- Multiply two large integers by Fast Fourier Transform
Computation records of Pi over the ages...
(in modern notations of course...)
note : 4*2+4*3 means Pi=4 arctan(1/2)+4arctan(1/3), it's the formula used to compute the digits (see Machin)
| NAME |
DATE |
Approx. or method used |
Good digits |
| Babylonians |
-2000 |
3+1/8=3,125 |
1 |
| Egyptians (scribe Ahmès) |
-1650 |
(16/9)2=3,16045 |
1 |
| Chinese |
-1200 |
3 |
0 |
| Bible |
-550 |
3 |
0 |
| Archimedes |
-250 |
3,14185 |
3 |
| Hon Han Shu |
130 |
1 |
|
| Ptolemy |
150 |
377/120=3,14166 |
3 |
| Chung Hing |
250 |
1 |
|
| Wang Fau |
250 |
142/45=3,155 |
1 |
| Liu Hui |
264 |
3,14159 |
5 |
| Siddhanta |
380 |
3+177/1250=3,1416 |
3 |
| Tsu Chung Chih |
480? |
355/113=3,141592 |
6 |
| Aryabhata |
499 |
3,14156 |
4 |
| Brahmagupta |
640 |
101/2=3,1622 |
1 |
| Al-Khowarizmi |
800 |
3,1416 |
3 |
| Fibonacci |
1220 |
3,141818 |
3 |
| Al-Kashi |
1429 |
6016I59II28III1IV34V51VI46VII14VIII50IX |
14 |
| Otho |
1573 |
3,1415929 |
6 |
| Viete |
1593 |
3,1415926536 |
9 |
| Romanus |
1593 |
|
15 |
| Van Ceulen |
1596 |
Archimedes' method |
20 |
| Van Ceulen |
1609 |
" |
34 |
| Grienberger |
1630 |
" |
39 |
| Newton |
1665 |
" |
16 |
| Sharp |
1699 |
" |
71 |
| Seki |
1700 |
" |
10 |
| Machin |
1706 |
16*5-5*239 (Machin) |
100 |
| De Lagny |
1719 |
4*2+4*3 (Euler) |
112 (out of 127 computed) |
| Takebe Katahiro |
1723 |
polygon with 1024 sides |
41 |
| Matsunaga |
1739 |
|
50 |
| Vega |
1794 |
20*7+8arctan(3/79) (Euler 1755) |
140 |
| Rutherford |
1824 |
16*5-4*70+4*99 |
152 (out of 208) |
| Strassnitsky, Dahse |
1844 |
4*2+4*5+4*8 |
200 |
| Clausen |
1847 |
8*3+4*7 (Hutton 1776) |
248 |
| Lehmann |
1853 |
8*3+4*7 |
261 |
| Rutherford |
1853 |
440 |
|
| Shanks |
1874 |
527 (sur 707) |
|
| Ferguson |
1945 |
12*4+4*20+4*1985 |
539 |
| Ferguson |
1947 |
|
620 |
| Ferguson |
1948 |
|
710 |
| Ferguson and wrench |
1948 |
|
808 |
| Smith and Wrench |
1949 |
|
1 120 |
| Reitwiesner on the ENIAC |
1949 |
2 037 |
|
| Nicholson and Jeenel |
1954 |
arctan formulae |
3 092 |
| Felton |
1957 |
32*10-4*239-16*515 |
7 480 |
| Genuys |
01-1958 |
|
10 000 |
| Felton |
05-1958 |
48*18+32*57-20*239 |
10 021 |
| Guilloud |
1959 |
|
16 157 |
| Shanks and Wrench |
1961 |
24*8+8*57+4*239 |
100 265 |
| Guilloud and Filliatre |
1966 |
|
250 000 |
| Guilloud and Dichampt |
1967 |
|
500 000 |
| Guilloud and Bouyer |
1973 |
formulae Störmer+ Gauss |
1 001 250 |
| Miyoshi and Kanada |
1981 |
|
2 000 036 |
| Guilloud |
1982 |
|
2 000 050 |
| Tamura |
1982 |
|
8 388 576 |
| Kanada, Yoshino and Tamura |
1982 |
|
16 777 206 |
| Gosper |
1985 |
Ramanujan's sum |
17 526 200 |
| Bailey |
01-1986 |
Borwein's algorithms (order 2 and 4) |
29 360 111 |
| Kanada and Tamura |
10-1986 |
Borwein's algorithms (order 2 and 4) |
67 108 839 |
| Kanada, Tamura, Kobo |
01-1987 |
" |
134 217 700 |
| Kanada and Tamura |
01-1988 |
" |
201 326 551 |
| Chudnovsky and Chudnovsky |
05-1989 |
Ramanujan's type sums |
480 000 000 |
| Chudnovsky and Chudnovsky |
06-1989 |
Ramanujan's type sums |
525 229 270 |
| Kanada and Tamura |
07-1989 |
Borwein's algorithms (order 2 and 4) |
536 870 898 |
| Chudnovsky and Chudnovsky |
08-1989 |
Ramanujan's type sums |
1 011 196 691 |
| Kanada and Tamura |
11-1989 |
Borwein's algorithms (order 2 and 4) |
1 073 741 799 |
| Chudnovsky and Chudnovsky |
08-1991 |
Ramanujan's type sums |
2 260 000 000 |
| Chudnovsky and Chudnovsky |
05-1994 |
Ramanujan's type sums |
4 044 000 000 |
| Kanada |
06-1995 |
Borwein's algorithms (order 2 and 4) |
4 294 967 286 |
| Kanada |
10-1995 |
Borwein's algorithms (order 2 and 4) |
6 442 450 938 |
| Takahashi-Kanada |
08-1997 |
Borwein's algorithms (order 2 and 4) |
51,539,600,000 |
| Takahashi-Kanada | 04-1999 |
algorithms Brent/Salamin |
68,719,470,000 |
| Takahashi-Kanada | 20-09-1999 | 206,158,430,000 soit environ 3.236 |
|
| Kanada | 06-12-2002 | 1,241,100,000,000 |
from D. Bailey, J. et P. Borwein, S. Plouffe and myself
Digits computed by hand then using a computer
Other plots from myself (in french but understandable I guess)
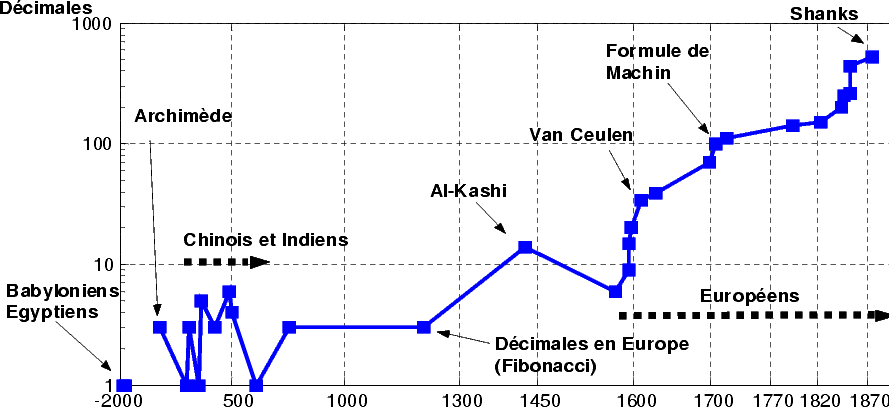
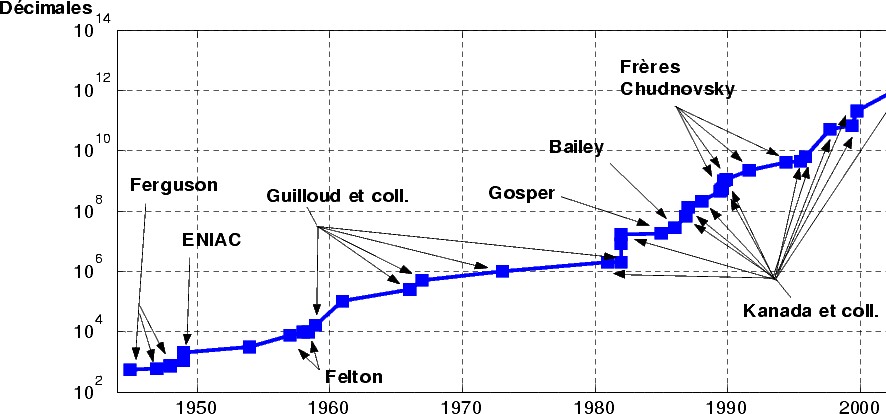
Place computed (digits in base 2 not knowing the previous ones)
| Bailey-Borwein-Plouffe |
1996 |
40 000 000 000 |
| Bellard |
7-6-1996 |
50 000 000 000 |
| Bellard |
10-7-196 |
100 000 000 000 |
| Bellard |
9-22-97 |
1 000 000 000 000 |
| Colin Percival - Project Pihex |
8-21-98 |
5 000 000 000 000 |
| Colin Percival - Project Pihex | 2-9-99 |
40,000,000,000,000 |
| Colin Percival - Project Pihex |
11-9-2000 |
1,000,000,000,000,000 |
Continued fraction for Pi
Main records :
| Gosper |
1977 |
17,001,303 |
| H. Havermann |
Juin 1999 |
20,000,000 |
| H. Havermann | Mars 2002 |
180,000,000 |
Note that Havermann has a very interesting page about the fraction expansion of Pi
Digits record in a classroom
Ok, I invented this class of records ;-)... however, this was to promote the work of the 7th grade (US-equivalent) classsroom located in Bouchain, north of France. They meet every monday in this 2012-2013 year to add digits and there are 85 of them so far ! Congratulations to them !! (Click on images to get high density pictures).
Pi memory records
A Japanese holds the record, just try to imagine what it means as memory, that crazy !
Main Pi memory records:
| Simon Plouffe |
1975 |
4096 |
| Hideaki Tomoyori |
1979 |
15,151 |
| Hiroyuki Goto (in 9h) |
1995 |
42,000 |
| Akira Haraguchi (details below) | 2006 |
100,000 |
 Akira Haraguchi, a 60-year old Japanese man, managed to recite 100 000 digits of Pi in 16h30 on October 3rd, 2006, breaking his own (unofficial) record of 83 431 digits established in 2005 ! First comment from Akira: "I don't think it's anything exceptional, I just emptied my mind of everything else and recited the numbers" ;-) Here is the BBC coverage, there the world-ranking of Pi memory (not up to date) and here the report about his previous record in 2005.
Akira Haraguchi, a 60-year old Japanese man, managed to recite 100 000 digits of Pi in 16h30 on October 3rd, 2006, breaking his own (unofficial) record of 83 431 digits established in 2005 ! First comment from Akira: "I don't think it's anything exceptional, I just emptied my mind of everything else and recited the numbers" ;-) Here is the BBC coverage, there the world-ranking of Pi memory (not up to date) and here the report about his previous record in 2005.
World records announcement (html)
1000 billion-th (10^12) binary digit of Pi by Fabrice Bellard- 22/09/97
5 000 billion-th digit of Pi is '0' by Colin Percival (project PiHex) - 21/08/98
40 000 billion-th digit of Pi is '0' by Colin Percival (project PiHex) - 9/02/99
The 1 000 000 billion-th binary digit of Pi (1015) is '0' by Colin Percival (project PiHex) - 11/09/00
51,539,600,000 digits of Pi by Kanada
08/06/97
206,158,430,208 (=3*2^36) digits of Pi by Kanada
04/10/99
About the world record of Takahashi-Kanada from april 1999 (68 719 470 000 digits)
Two computations on a HITACHI SR8000 based on two independant algorithms ( Brent/Salamin and fourth-order algorithm from the Borwein) generated 68,719,476,736 (=236) digits of Pi. Comparing the two results, they found 68,719,476,693 common digits. The new record has thus been established to 68,719,470,000 digits of Pi.
Main program:
Starting : April 2nd, 1999 8pm:14:38
End : April 4th, 1999 5am:08:41
Total time: 32:54:02
Memory used: 296 GB
Algorithm : Gauss-Legendre (Brent-Salamin)
Checking program :
Starting : 4th April 1999 5am:08:48
End : 5th April 1999 8pm:29:25
Total time: 39:20:37
Memory used : 280 GB
Algorithm : fourth order from Borwein
About the world record of Kanada from september 1999 (206,158,430,000 digits)
Two computations on a HITACHI SR8000 based on two independant algorithms ( Brent/Salamin and fourth-order algorithm from the Borwein) generated 206,158,430,208 (=3.2^36) digits of Pi. Comparing the two results, they found 206,158,430,163 common digits. The new record has thus been established to 206,158,430,000 digits of Pi.
Main program:
Starting : September 18th, 1999 7pm:00:52 (Japan time)
End : September 20th, 1999 8am:21:56
Total time: 37:21:04
Memory used: 865 GB (=6.758*128)
Algorithm : Gauss-Legendre (Brent-Salamin)
Checking program :
Starting : June 26th, 1999 1am:22:50
End : June 27th, 1999 11pm:30:40
Total time: 46:07:10
Memory used : 817 GB (=6,383*128)
Algorithm : fourth order from Borwein
About the world record of Kanada from december 2002 (1,241,100,000,000 digits)
Two computations lasting 600 hours on a HITACHI SR8000/MP with 1TB storage (1024Go), and based on two independent Machin-like formulas, generated 1,241,100,000 digits of Pi after that the result obtained in hexagesimal base was converted to base 10. Formulae used were :
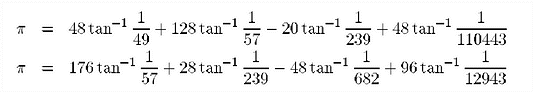
This come back of amazingly simple formulae after using Brent-Salamin, Borwein algorithms or Ramanujan-like formulae for 15 years was highly unexpected. Actually, despite the algorithmic improvements, the complexity of these latter formulae had reached computer limits. Indeed, the widely use of root extractions and multiplications required the common use of very large scale Fast Fourier Transform (FFT). This algorithm needs huge memory. Kanada thus decided to be wiser and to use Machin-like formulas which need more arithmetical operations with much less very large scale FFT and so less memory. It seems that similar issues start to appear in the fastest computers in the world whose network and memory operations saturate faster than what was expected theoretically. Kanada estimates than his computation is twice faster than the previous one using Brent/Salamin and Borwein algorithms.
Some papers about this record :
Kanada's lab with several articles in "Press Release"
Page of J. Borwein about this record
MathTrek (Ivan Peterson)
A few statistics on Pi
Frequency of digits on the first 50 000 000 000 digits:
'0' : 5000012647
'1' : 4999986263
'2' : 5000020237
'3' : 4999914405
'4' : 5000023598
'5' : 4999991499
'6' : 4999928368
'7' : 5000014860
'8' : 5000117637
'9' : 4999990486
Chi square = 5.60
Frequency of digits of 1/Pi on the first 50,000,000,000 digits:
'0' : 4999969955
'1' : 5000113699
'2' : 4999987893
'3' : 5000040906
'4' : 4999985863
'5' : 4999977583
'6' : 4999990916
'7' : 4999985552
'8' : 4999881183
'9' : 5000066450
Chi square = 7.04
On this page, you can also download 1 million digits !
- Display
(HTML) (1.1 Mo)
- Download (stuffit) (488Ko)
- Download (zip) (528Ko)
If you want more....
- Download 4 200 000 000 digits
The first 1000 digits just for fun....
3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679
8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196
4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273
7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094
3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912
9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132
0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235
4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859
5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303
5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989...
back to home page






