back to home page

Al Kashi
(? - 1429)

Slices of life

His real name was "ghiyat al-dîn djamashîd b.mahs'ûd b.mahmûd al Kashi" (very short !) but he is more known under the shortened name of Al Kashi, from his birthplace Kachan between Ispahan and Teheran. Famous mathematician of his time, he died in Samarkand in 1429. His major work, the treaty of the circle (Risala has - muhitiyya), was written in Arabic in 1424.

About

In this manuscript, although there has been nothing really new since Archimedes, its calculus virtuosity incites him to dash a challenge: calculate a good estimation of 2 (ratio between the circumference of the circle and its radius). "Good" means for him that for a circle 600 000 times big as the earth equator, uncertainty must be lower than " a hair of horse ". That represents 16 exact decimals of or 10 sexagesimal places in the base 60 used by Al Kashi. Indeed, Al Kashi exhibits 6 ⁰16 ^I59 ^II28 ^III1 ^IV34 ^V51 ^VI46 ^VII14 ^VIII50 ^IX !

Proof

Usually at this time, method used by Al Kashi is Archimedes' one, because Al Kashi starts from a hexagon and thus from one side of length 2sin(/6)=1. We then pose

C_n=

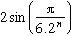
By equivalence of x and sin(x) if x tends towards 0, 3.2ⁿ.C_n tends towards when n goes to infinity.
We then can find a recurrence relation from the trigonometry formulae cos²(x)+sin²(x)=1, and cos(x)=1-2sin²(x/2). We have . The latter relation gives the final relation with C_n by replacing x by /(6.2ⁿ) .

Trials

The formula being almost the same than Archimedes' one with just a factor 2 difference, trials and performances are perfectly similar! It's the same for the acceleration of the convergence by Aitken's Delta2.