Archimedes
(287 av. J.-C. - 212 av. J.-C.)

Application of Archimedes' method:

Slices of life :

Archimedes was born in about 287 BC. Considered by all as the greatest mathematician and physicist of all the antiquity (and it is justified!), the legend which surrounds him and the papers which reached us are indeed rather impressive! De l'Equilibre des plans, Sur la sphère et le cylindre, l'Arénaire - where Archimedes exposes a system of numbering of the great numbers (calculation of the number of grains of sand contained in the sphere of the world!!!)-, Traité de la méthode, are so much brilliant papers. Without forgetting naturally Des corps flottants - and his famous Archimedes's principle-, and the la Mesure du cercle. In this last work which interests us, Archimedes shows the famous bounding

Leading the defence of Syracuse against Romans ( we attribute to him, but debate is lively, to have been able to set on fire in distance the fleet of Marcellus by means of a game of mirrors) and in spite of the orders of protection of a Roman general, he is murdered by a legionary during the capture of the city in 212 BC. And for which motive, will you say to me? Well, according to the legend, Archimedes was drawing a figure on the ground, and says to the Roman which entered not to disturb him. This last one, hurt, would have pierced him with its lance. But the wealth of Archimedes's home was there maybe also for something...

About

Archimedes had naturally never under the eyes the formula above, moreover he did not know trigonometry ! Nevertheless, this one is only a modern writing of its approximation method of Pi. Oh yes, this good old Archimedes was indeed the first to calculate really its decimal by means of an algorithm. he start from 2 polygons of 6 sides inscribed and circumscribed in a circle of radius R=1/2. Doubling every time the number of sides of polygons, these last ones were going eventually become merged with the circle, and their perimeter was going to tend towards the perimeter of the circle, is 2xPixR. Brilliant idea which will prevail in the calculation of the decimal until XVII-th century!
His method may be presented in different algorithmic forms, like this one (see also Cues, Al Kashi, Viète);
Archimedes obtained his frame with a polygon of 96 sides (n=4 in the formula).

Proof

A circle of radius 1 and an angle of are considered . Let put . Un represent the length of one side of the polygon inscribed in the circle and Vn the length of the polygon circumscribed in the circle.
By limited developments in 0, so we obtain the result of the formula in the top of the page at once.

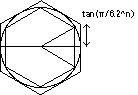
This reasoning of pure analysis was translated geometrically for Archimedes by the fact that the polygon in 6.2n sides tends to become merged with the circle when n tends to the infinity. We have to Un and Vn has the same form that in the formula...

To do it, it is enough to look for a formula of recurrence between Un+1 and Un (Positive) on the one hand, and starting from Vn+1 And Vn (Positive also) on the other hand.
From cos ² X+sin ² X=1 and cos(2x)=1-2.sin ²(X), we obtain what gives relation

.

Also, we have , so by putting X=, we have the trinomial of the second degree in X.
tan(x).X² +2X-tan(x)=0. Positive solution gives X=tan(x/2)= which gives for all positive integer n. The value of U0 and V0 is obtained by the first expressions of Un And Vn .

Trials

Small note about attempts : These are only a better way to feel the performances of a series. To be clear, I shall use a little personal but so practical notation! When a convergence will be found "about 3n/5" as here, it will mean that we will have about 3n/5 decimal right at rank n. It does not have anything to see with a "convergence in n*log (n)" for example which means that the time of calculation of n decimal is proportional in n*log (n).
The figure in brackets indicates the number of decimal right.

U1=3,10582 (1)	V1=3,21539 (0)
U4=3,14103 (3)	V4=3,14271 (2) (bounding of Archimedes)
U10=3,14159251 (6)	V10=3,14159296 (6)

We observes a convergence about 3n/5 for 2 series that is very honourable with regard to series with logarithmic convergence (Wallis, Stirling...). . This explains doubtless also that this method prevailed so for a long time to calculate the decimals of (Oh, just a little while, 20 centuries (!), until the discovery of the formula of Machin in 1706).

Acceleration of the convergence

As in about every mathematicians' web page of this site, we will find a chapter dedicated to the acceleration by Aitken's Delta2, so much this formula is effective and simple to apply.
For n=5, we have U5 =3,14145 (3) and t5 =3,1415926836 ( 7 ).
Impressive, 4 decimals are gained, in fact, we double the speed of convergence, that is much more economical than to calculate the 6 iterations of Un supplementary that we would need otherwise to obtain the same number of decimals...
For n=7, we have U7 =3,141583 (4) and t7=3,14159265370 (9).
(remember nevertheless that Delta2 is very sensitive to imprecision...)