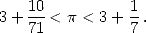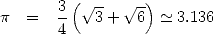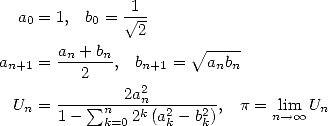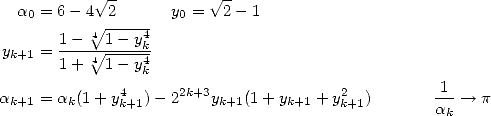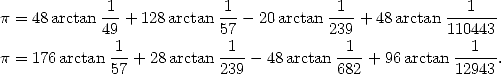|
|
|
|
|

Pi-Story ou l’histoire du nombre Pi
Intro vraiment courte :
Intro plus sérieuse !
1
 dans l’antiquité
dans l’antiquité
2 Ah enfin l’analyse ! (XVIIIe siècle - fin XIXe siècle)
3 L’ordinateur prend le relais
4 L’approche BBP, encore du nouveau sur
5 Une quête sans fin ?
References
Pages associées
- Page des mathématiciens (lien sur chacun de leur nom)
- Algorithme de Newton
- Multiplication de grands entiers par Transformée de Fourier Rapide
- Atteindre le n-ième digit de Pi sans connaître les précédents (méthode de Plouffe)
- Records de décimales de Pi au cours des siècles
Intro vraiment courte :
 est une constante qui trouve ses origines dans la lointaine antiquité. Que de chemin parcouru jusqu’à ce
jour !
est une constante qui trouve ses origines dans la lointaine antiquité. Que de chemin parcouru jusqu’à ce
jour !
L’histoire de la constante s’étale sur quatre périodes bien distinctes durant lesquelles l’esprit et les
méthodes associés à 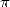 furent bien différents. On retient essentiellement :
furent bien différents. On retient essentiellement :
1. 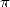 dans l’antiquité
dans l’antiquité
* Antiquité - XVIIe siècle : la méthode géométrique d’Archimède triomphe
2. Ah, enfin l’analyse !
* XVIIIe - début XXe : c’est le temps des découvertes et des formules dans tous les sens !
3. Les ordinateurs au travail...
* XXe siècle : avec les équations de Ramanujan et les ordinateurs, on peut repousser les limites du calcul.
4. Promenons-nous dans les décimales
* A l’approche du millénaire, Plouffe fait sa révolution !
Intro plus sérieuse !
Le nombre 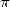 occupe une place très particulière dans le monde mathématique, et sans cesse réaffirmée. Il
peut se targuer d’avoir occupé l’esprit des mathématiciens dès l’antiquité, et comme le disent Bergrenn et les
frêres Borwein [6], le calcul de ses décimales est probablement le seul problème apparu dès les prémices des
mathématiques, et qui soit encore d’actualité dans la recherche moderne. Pourtant, les motivations associées
ont sensiblement évolué au cours des siècles.
occupe une place très particulière dans le monde mathématique, et sans cesse réaffirmée. Il
peut se targuer d’avoir occupé l’esprit des mathématiciens dès l’antiquité, et comme le disent Bergrenn et les
frêres Borwein [6], le calcul de ses décimales est probablement le seul problème apparu dès les prémices des
mathématiques, et qui soit encore d’actualité dans la recherche moderne. Pourtant, les motivations associées
ont sensiblement évolué au cours des siècles.
D’abord liées au besoins pratiques et quotidiens des anciens, les évaluations toujours plus
précises du nombre 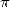 ont ensuite découlé, presque comme un jeu, des découvertes successives
et foisonnantes de formules d’analyse toujours plus efficaces de la renaissance jusqu’au XIXe
siècle.
ont ensuite découlé, presque comme un jeu, des découvertes successives
et foisonnantes de formules d’analyse toujours plus efficaces de la renaissance jusqu’au XIXe
siècle.
La révolution des ordinateurs au XXe siècle changea ensuite complètement la donne : l’attrait du calcul ne
venait plus du résultat en lui-même, mais de la manière de l’obtenir, du point de vue des techniques
mathématiques et algorithmiques. Un nouveau changement de cap a fait son apparition depuis
1996, qui tente de mettre en relation les expressions analytiques de 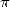 et la structure profonde
de ses décimales. De ce champ d’explorations à la frontière de la théorie de la complexité ont
éclos quelques conjectures encore ouvertes sur la nature “aléatoire” de nombreuses constantes
mathématiques (
et la structure profonde
de ses décimales. De ce champ d’explorations à la frontière de la théorie de la complexité ont
éclos quelques conjectures encore ouvertes sur la nature “aléatoire” de nombreuses constantes
mathématiques (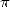 ,
,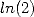 , etc...). D’autres conséquences jusqu’ici insoupçonnées, comme la possibilité
d’atteindre dans certaines bases le n-ième digit de
, etc...). D’autres conséquences jusqu’ici insoupçonnées, comme la possibilité
d’atteindre dans certaines bases le n-ième digit de 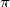 sans connaitre les précédents avec peu
de mémoire et de temps, ont renouvelé l’attrait du calcul des digits ou décimales du nombre
sans connaitre les précédents avec peu
de mémoire et de temps, ont renouvelé l’attrait du calcul des digits ou décimales du nombre
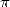 .
.
Cette page se propose de revenir sur ces quatre périodes charnières (Antiquité, 18e/19e siècle, 20e siècle, et
depuis 1996) en expliquant les cheminements de pensée et les méthodes de calcul qui ont conduit à
connaître plus de 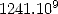 décimales de
décimales de 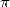 en ce début de troisième millénaire ! Nous achèverons
cette synthèse par un petit état des lieux des motivations actuelles de calcul des décimales de
en ce début de troisième millénaire ! Nous achèverons
cette synthèse par un petit état des lieux des motivations actuelles de calcul des décimales de
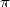 .
.
1 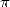 dans l’antiquité
dans l’antiquité
Avec Pi, la machine à explorer le temps est une réalité... Mais bien sûr, pour plus de commodités, le langage
moderne et habituel des mathématiques est utilisé ici... Il ne faut pas croire que les Babyloniens écrivaient et
les nombres en décimales. Ils ne connaissaient même pas la trigonométrie et utilisaient la base 60 au lieu
de la base 10, en notation fractionnaire (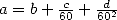 ). De plus, les signes +, =,
). De plus, les signes +, =, ,
,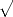 n’ont été inventés que pendant la renaissance, les écritures de l’antiquité ressemblaient plus à du
langage écrit qu’autre chose. Les égyptiens avaient un peu d’avance puisqu’ils utilisaient le système
décimal, manipulaient les fractions de numérateur 1, et avaient inventé un signe + (deux jambes
vers la gauche) et le - (deux jambes vers la droite). Cela étant dit, retournons aux origines de la
légende...
n’ont été inventés que pendant la renaissance, les écritures de l’antiquité ressemblaient plus à du
langage écrit qu’autre chose. Les égyptiens avaient un peu d’avance puisqu’ils utilisaient le système
décimal, manipulaient les fractions de numérateur 1, et avaient inventé un signe + (deux jambes
vers la gauche) et le - (deux jambes vers la droite). Cela étant dit, retournons aux origines de la
légende...
1.1 Du haut des pyramides, 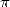 nous contemple !
nous contemple !
On me demande parfois en quelle année a-t-on découvert 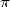 ! Je ne sais pas répondre à cette question car
c’est le résultat d’un long processus. Les anciens avaient essentiellement besoin de la géométrie pour les
mesures de surface de terre, ou dans l’architecture, par exemple pour évaluer la taille et la proportion des
bâtiments. Selon l’historien grec Herodote, on pouvait trouver de nombreuses relations géométriques dans les
pyramides de Gizeh, à qui il rendit visite vers 450 AV. J.C. (soit plus de 2000 ans après leur
construction tout de même !). Par exemple, un principe de construction voulait que l’aire de chaque
surface latérale soit égale à l’aire d’un carré de côté égal à la hauteur de la pyramide (ce qui
est vrai à 0.7% près pour la pyramide de Kheops !). De nombreuses constantes apparaissent
ainsi de manière quasi-magique, puisque le rapport de la hauteur sur le côté de la base de la
pyramide vaut
! Je ne sais pas répondre à cette question car
c’est le résultat d’un long processus. Les anciens avaient essentiellement besoin de la géométrie pour les
mesures de surface de terre, ou dans l’architecture, par exemple pour évaluer la taille et la proportion des
bâtiments. Selon l’historien grec Herodote, on pouvait trouver de nombreuses relations géométriques dans les
pyramides de Gizeh, à qui il rendit visite vers 450 AV. J.C. (soit plus de 2000 ans après leur
construction tout de même !). Par exemple, un principe de construction voulait que l’aire de chaque
surface latérale soit égale à l’aire d’un carré de côté égal à la hauteur de la pyramide (ce qui
est vrai à 0.7% près pour la pyramide de Kheops !). De nombreuses constantes apparaissent
ainsi de manière quasi-magique, puisque le rapport de la hauteur sur le côté de la base de la
pyramide vaut 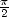 à 1,7% près. Ces coïncidences remarquables sont parfois contestées mais restent
fascinantes.
à 1,7% près. Ces coïncidences remarquables sont parfois contestées mais restent
fascinantes.
Le plus ancien objet où 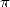 intervient plus ou moins implicitement est une tablette babylonienne en
écriture cunéiforme, découverte en 1936 et qui remonte à la période 1900-1600 avant J.C. Elle évalue le
périmètre d’un hexagone à
intervient plus ou moins implicitement est une tablette babylonienne en
écriture cunéiforme, découverte en 1936 et qui remonte à la période 1900-1600 avant J.C. Elle évalue le
périmètre d’un hexagone à 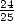 fois celui du cercle circonscrit (soit
fois celui du cercle circonscrit (soit ![[0,57,36]](../histoire/histoire24x.gif) dans leur base
dans leur base 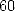 dont il nous
reste le décompte des secondes/minutes), ce qui revient à estimer
dont il nous
reste le décompte des secondes/minutes), ce qui revient à estimer 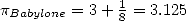 . C’est
officiellement la plus vieille approximation connue de
. C’est
officiellement la plus vieille approximation connue de 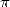 !
!
De même, pour revenir aux égyptiens, le célèbre papyrus de Rhind rédigé en écriture hiératique et
découvert en 1855 par A. H. Rhind à Louxor relate une série de problèmes anciens recopiés par
le scribe Ahmes. Le n affirme que l’aire d’un disque de diamètre
affirme que l’aire d’un disque de diamètre 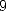 est égale à 64 , soit
le carré du diamètre auquel on a retiré
est égale à 64 , soit
le carré du diamètre auquel on a retiré 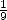 de sa longueur
de sa longueur 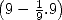 . Ceci revient à estimer
. Ceci revient à estimer
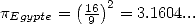 . Ils sont probablement parvenus à cette idée en approximant l’aire de ce disque
par celle d’un octogone partitionné en carrés et triangles de côté 1, et qui donne alors une aire
de 63 (problème n
. Ils sont probablement parvenus à cette idée en approximant l’aire de ce disque
par celle d’un octogone partitionné en carrés et triangles de côté 1, et qui donne alors une aire
de 63 (problème n 48). Notons que les Egyptiens ne travaillaient qu’avec des fractions de la
forme
48). Notons que les Egyptiens ne travaillaient qu’avec des fractions de la
forme 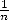 et qu’ils avaient donc opté pour la meilleure des approximations de ce genre puisque la
diminution du
et qu’ils avaient donc opté pour la meilleure des approximations de ce genre puisque la
diminution du  est meilleure que la diminition du
est meilleure que la diminition du 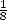 . Remarquons tout de même (soyons
beaux joueurs !) que ces moyens rudimentaires ont fourni des valeurs correctes à moins d’1%
près. Le même genre de méthodes sera appliqueé en Inde (600 av. J.C.) ou en Chine (150 ap.
J.C.).
. Remarquons tout de même (soyons
beaux joueurs !) que ces moyens rudimentaires ont fourni des valeurs correctes à moins d’1%
près. Le même genre de méthodes sera appliqueé en Inde (600 av. J.C.) ou en Chine (150 ap.
J.C.).
Dans l’antiquité, on s’est visiblement rendu compte assez vite que le rapport du périmètre d’un cercle sur son diamètre était constant. Nous savons par ailleurs que les Egyptiens avaient compris que le rapport lié au périmètre d’un cercle et celui lié à l’aire du cercle étaient les mêmes.
 |
| Le papyrus de Rhind conservé au British Museum (1800-1650 av. JC) |
Nous ne savons pas si c’était le cas des Babyloniens, ni même si ces civilisations avaient conscience de
n’avoir obtenu qu’une valeur approchée de 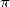 . Il faut noter que la diffusion des connaissances étant plutôt
réduite à cette époque, de nombreuses autres approximations, parfois bien plus mauvaises ont éclot même
après la découverte de ces premières valeurs. Ainsi, après les Egyptiens et les Babyloniens, c’est un peu le
vide... Les Chinois vers -1200 donnent 3 pour valeur, ce qui dénote tout de même un certain manque de
recherches sur le sujet ! La Bible, manquant un peu d’inspiration divine pour l’occasion, fournit elle aussi 3
pour valeur de
. Il faut noter que la diffusion des connaissances étant plutôt
réduite à cette époque, de nombreuses autres approximations, parfois bien plus mauvaises ont éclot même
après la découverte de ces premières valeurs. Ainsi, après les Egyptiens et les Babyloniens, c’est un peu le
vide... Les Chinois vers -1200 donnent 3 pour valeur, ce qui dénote tout de même un certain manque de
recherches sur le sujet ! La Bible, manquant un peu d’inspiration divine pour l’occasion, fournit elle aussi 3
pour valeur de 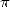 vers -550 av. J.C.. Le passage du fondeur Hiram et de son chaudron est resté célèbre, le
voici en termes francisés : "Il fit aussi une mer de fonte de dix coudées d’un bord jusqu’à l’autre, qui était
toute ronde : elle avait cinq coudées de haut et était environnée tout à l’entour d’un cordon de trente
coudées". 30/10=3, pas d’erreur. On dira bien plus tard que le passage concernait le contour
intérieur du chaudron pour calmer les polémiques, mais l’absence de besoin de précision pour les
fondeurs semble être la seule justification... Heureusement, voilà les Grecs qui vont remettre un peu
d’ordre...
vers -550 av. J.C.. Le passage du fondeur Hiram et de son chaudron est resté célèbre, le
voici en termes francisés : "Il fit aussi une mer de fonte de dix coudées d’un bord jusqu’à l’autre, qui était
toute ronde : elle avait cinq coudées de haut et était environnée tout à l’entour d’un cordon de trente
coudées". 30/10=3, pas d’erreur. On dira bien plus tard que le passage concernait le contour
intérieur du chaudron pour calmer les polémiques, mais l’absence de besoin de précision pour les
fondeurs semble être la seule justification... Heureusement, voilà les Grecs qui vont remettre un peu
d’ordre...
1.2 Eureka !! : le principe d’exhaustion chez les grecs
Les mathématiciens grecs de l’antiquité sont souvent considérés comme les premiers à réellement se soucier des démonstrations. Les problèmes qui les occupaient restaient cependant majoritairement géométriques. Parmi eux, le problème de construire un carré de même aire qu’un cercle (la célèbre quadrature du cercle) fut initié, au moins historiquement, par Anaxagore de Clazomène (500-428 avant J.C.) pendant un séjour en prison pour impiété (il osait soutenir en particulier que la lune ne faisait que refléter la lumière du soleil ! Ça ne rigolait pas en ce temps là !). Si de nombreuses solutions furent alors proposées, le problème devint insoluble pendant 23 siècles quand Euclide ajouta comme conditions de le résoudre uniquement :
Le lien entre ces conditions et les propriétés algébriques des nombres qui en découlent ne fut proprement énoncé qu’en 1837 par Pierre Laurent Wantzel :
Theorem 1.1 Les nombres finiment définissables à l’aide de la règle et du compas sont les grandeurs définissables par opérations algébriques simples (addition, multiplication, extraction de racines...) autrement dit par radicaux.
Bien que les nombres définis par radicaux soient algébriques (racines de polynômes à coefficients dans 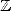 ),
Abel montra en 1824 que tous les nombres algébriques ne sont pas toujours exprimables par radicaux dès que
le degré du polynôme atteint 5, et Liouville démontra en 1851 l’existence de nombres non algébriques, i.e.
transcendants. Le problème de la quadrature du cercle se ramena donc rapidement au milieu du XIXe siècle à
celui de la transcendance de
),
Abel montra en 1824 que tous les nombres algébriques ne sont pas toujours exprimables par radicaux dès que
le degré du polynôme atteint 5, et Liouville démontra en 1851 l’existence de nombres non algébriques, i.e.
transcendants. Le problème de la quadrature du cercle se ramena donc rapidement au milieu du XIXe siècle à
celui de la transcendance de 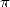 .
.
La distance qui séparait les conceptions géométriques grecques de l’expression formelle du problème de la
quadrature du cercle explique la lente maturation des mathématiciens vers la démonstration finale et
rigoureuse de la transcendance de 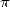 en 1882 par Lindemann , qui clotura ce débat vieux de plus de 23
siècles !
en 1882 par Lindemann , qui clotura ce débat vieux de plus de 23
siècles !
Avec les outils dont disposaient les grecs, les solutions proposées à la quadrature du cercle faisaient la plupart du temps appel à un nombre infini d’étapes comme la quadratrice de Dinostrate, construite initialement par Hippias d’Elis vers 430 avant J.C., ou encore la méthode d’exhaustion.
Cette dernière est généralement attribuée à Antiphon (vers 430 avant J.C.) ou Eudoxe de Cnide (408-355
avant J.C.), et consiste à construire un polygone dont le nombre de côtés augmenterait jusqu’à ce qu’il
devienne indiscernable du cercle. Cette brillante idée se heurte néanmoins au manque de notion de limite à
l’époque. On sait aujourd’hui que ce n’est pas parce qu’une propriété est vraie pour tout 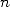 entier qu’elle l’est
à la limite (
entier qu’elle l’est
à la limite (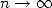 ). Autrement dit, même si un polygone à
). Autrement dit, même si un polygone à 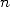 côtés est quarrable, cela ne signifie pas que
sa limite - le cercle - le soit aussi, contrairement à l’idée d’Antiphon. Le brillant Euclide (330-275 avant J.C.)
écrit néanmoins qu’en considérant un polygone avec un grand nombre de côtés, on peut “rendre
la différence entre l’aire à calculer et l’aire des polygones qu’on construit plus petite que toute
quantité positive pré-assignée, aussi petite soit-elle” (d’après [12]), ce qui est une conception
étonnament proche de la formalisation des limites dans les mathématiques du XIXe siècle. Il en
déduisit d’ailleurs que l’aire du cercle était proportionnelle au carré de son diamètre (Elements
12.2).
côtés est quarrable, cela ne signifie pas que
sa limite - le cercle - le soit aussi, contrairement à l’idée d’Antiphon. Le brillant Euclide (330-275 avant J.C.)
écrit néanmoins qu’en considérant un polygone avec un grand nombre de côtés, on peut “rendre
la différence entre l’aire à calculer et l’aire des polygones qu’on construit plus petite que toute
quantité positive pré-assignée, aussi petite soit-elle” (d’après [12]), ce qui est une conception
étonnament proche de la formalisation des limites dans les mathématiques du XIXe siècle. Il en
déduisit d’ailleurs que l’aire du cercle était proportionnelle au carré de son diamètre (Elements
12.2).
 |
| Deux pages des Éléments d’Euclide |
 |
| Euclide (365-300 av. J.C.) |
Il faut cependant attendre Archimède (287-212 avant J.C.) et son traité “De la mesure du cercle” pour
que cette idée soit efficacement appliquée à l’évaluation de 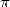 . Le premier de ses 3 théorèmes énonce que le
rapport de l’aire d’un disque au carré de son rayon est égal au rapport du périmètre à son diamètre. Le
troisième énonce explicitement que
. Le premier de ses 3 théorèmes énonce que le
rapport de l’aire d’un disque au carré de son rayon est égal au rapport du périmètre à son diamètre. Le
troisième énonce explicitement que
 |
| Archimède (287-212 av J.C.) |
Reprenant le principe d’exhaustion, il exhibe une relation formelle entre le périmètre du polygone à 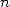 côtés et celui à
côtés et celui à 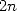 côtés (voir page Archimède). Partant de deux hexagones respectivement inscrit et
circonscrit, il obtient l’approximation 1 avec deux polygones à 96 côtés ! Ce calcul absolument sidérant fut
mené sans aucune notation algébrique, numération cohérente (les grecs utilisaient une numération additive
comme les romains), ni connaissance de la trigonométrie, et avec la seule géométrie d’Euclide. Il se formalise
aujourd’hui comme suit : Soient
côtés (voir page Archimède). Partant de deux hexagones respectivement inscrit et
circonscrit, il obtient l’approximation 1 avec deux polygones à 96 côtés ! Ce calcul absolument sidérant fut
mené sans aucune notation algébrique, numération cohérente (les grecs utilisaient une numération additive
comme les romains), ni connaissance de la trigonométrie, et avec la seule géométrie d’Euclide. Il se formalise
aujourd’hui comme suit : Soient 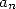 et
et 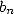 les demi-périmètres des polygones à
les demi-périmètres des polygones à 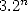 côtés respectivement
circonscrit et inscrit à un cercle de rayon 1. L’hexagone fournit
côtés respectivement
circonscrit et inscrit à un cercle de rayon 1. L’hexagone fournit 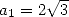 et
et 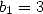 . On a ensuite les
formules de récurrence
. On a ensuite les
formules de récurrence
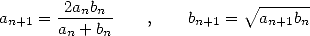 | (2) |
qui donnent 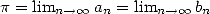 . Archimède poussa ses calculs jusqu’à
. Archimède poussa ses calculs jusqu’à 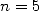 . Les cas
. Les cas 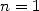 et
et
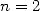 sont illustrés sur la figure ci-dessous.
sont illustrés sur la figure ci-dessous.
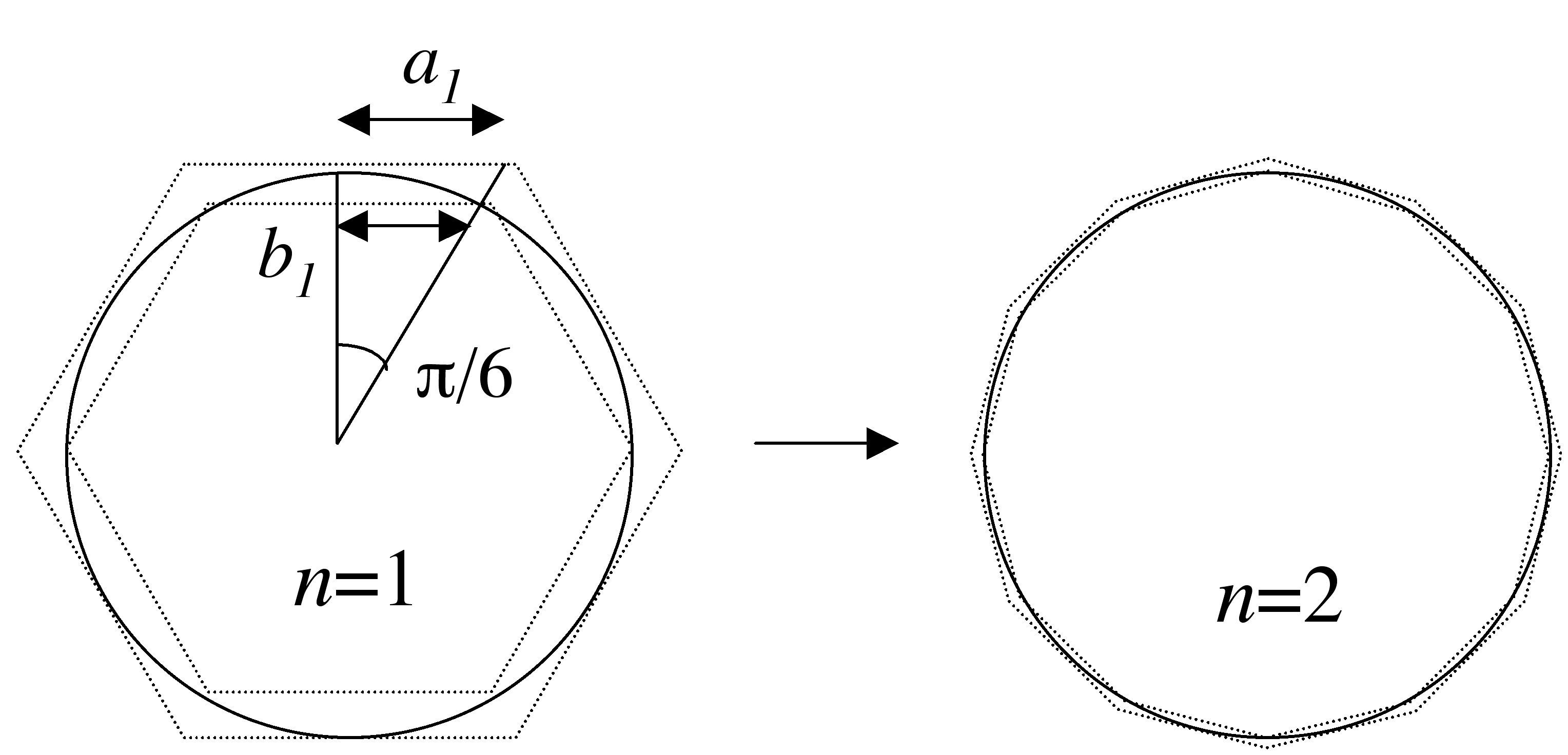 |
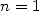 et et 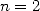 de l’itération d’Archimède de l’itération d’Archimède |
La démonstration de la convergence et de l’adjacence des deux suites est immédiate si l’on remarque que
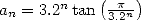 et
et 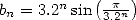 . On obtient alors
. On obtient alors
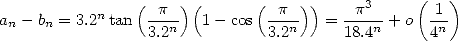 | (3) |
ce qui assure un nombre de décimales correctes égal à  itérations environ (3 décimales en 5 étapes). On
qualifiera cette convergence de linéaire. Le rayonnement d’Archimède était déjà tel pour l’époque, que
Tropfke [25] affirme que la valeur
itérations environ (3 décimales en 5 étapes). On
qualifiera cette convergence de linéaire. Le rayonnement d’Archimède était déjà tel pour l’époque, que
Tropfke [25] affirme que la valeur  remplaça rapidement à Alexandrie la vieille
valeur
remplaça rapidement à Alexandrie la vieille
valeur  =
=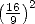 , d’usage aussi aisé mais moins précise, et se répandit jusqu’en Inde et même en
Chine au 5ème siècle après J.C. Ptolémée améliorera quelque peu le résultat au moyen de tables
trigonométriques.
, d’usage aussi aisé mais moins précise, et se répandit jusqu’en Inde et même en
Chine au 5ème siècle après J.C. Ptolémée améliorera quelque peu le résultat au moyen de tables
trigonométriques.
1.3 Voyage, voyage...
Après Archimède, la nuit mathématique tombe sur l’Occident pendant 1500 ans... Il est vrai que le système numérique des romains par exemple est peu propice aux calculs (tentez donc de multiplier LVIII par XCVI !) et ceux-ci ne vont donc pas laisser grand chose derrière eux côté ouvrages de mathématiques. Mais il se passe des choses ailleurs. Même si les mathématiciens asiatiques, arabes ou indiens se contenteront d’appliquer la même méthode qu’Archimède, ou une variante légère pendant près de 20 siècles, ils proposent des approximations toujours meilleures. Ainsi, en Inde, on travaille aussi puisque Aryabhata propose, vers 500 ap. J.C., 3 décimales exactes. Mais c’est en Chine où le système décimal a toujours été utilisé, que les progrès sont les plus rapides. Tsu Chung Chih semble être le premier à avoir proposé la fraction célèbre 355/113 = 3,14159292... vers 480 ap. J.-C. soit 6 décimales. Les Arabes et Perses ne sont pas en reste puisque dans son système Hexagésimal, Al Kashi calcule avec virtuosité 10 digits soit 14 décimales en 1429... Record absolu !
 |  |  |
| Aryabhata (476-550) | Tsu Chung-Chi (430-501) | Al-Kashi (1390-1450) |
Mais la notation décimale commence lentement à s’imposer en Europe au Moyen Âge et c’est alors tout
naturellement que l’Occident se réveille : c’est Fibonacci, l’un des seuls grands mathématiciens de
l’époque et adepte de la notation décimale, qui s’illustre tout d’abord et obtient 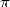 =3,1418...
mouais...
=3,1418...
mouais...
 |
| Fibonacci (1175-1250) |
Notons aussi que l’on ne cernait pas encore précisément le côté transcendant de Pi (mais c’est un peu normal...) puisque Nicolas de Cues propose au XVe siècle
Regiomontanus démontrera (!) que cette valeur est erronée... Nicolas de Cues avait utilisé une variante de la méthode d’Archimède.
 |
| Nicolas de Cues (1401-1464) |
De temps en temps, certains tentent cependant l’originalité. Ainsi, Descartes (1596-1650) prend le problème carrément à l’envers et propose sa méthode des isopérimètres qui fait non plus évoluer le périmètre des polygones mais bien le diamètre de ces polygones, dont le périmètre est alors fixé. Viete dérive également un premier produit infini en 1593 (sans le démontrer, mais bon, ce n’est guère l’époque !) en se penchant sur l’aire et non plus le périmètre:
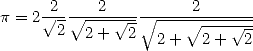 | (5) |
Mais la convergence est si lente qu’il préfère encore utiliser la méthode d’Archimède pour calculer lui-même 9 décimales en 1593.
 |  |
| René Descartes (1596-1650) | Viete (1540-1603) |
Avec simplement 1000 ans de retard sur les Chinois et Tsu Chung Chih, mais c’est son nom qui est resté,
Adrian Anthonisz fait la moyenne des valeurs d’encadrement calculées par Archimède et retrouve
355/113=3.14159292... C’est en tout cas ce que nous rapporte son fils qui a publié le résultat
en 1625. Ces valeurs semblaient tenues pour exactes pour 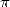 . Depuis les grecs, on savait qu’il
existait des nombres plus compliqués que les rationnels (irrationnels) comme
. Depuis les grecs, on savait qu’il
existait des nombres plus compliqués que les rationnels (irrationnels) comme 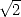 . On sentait
sans doute que
. On sentait
sans doute que 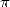 était d’une nature encore plus complexe, mais on tentait tout de même de
l’exprimer en fonction de nombres simples. Pendant ce temps, la numérotation décimale fait vite
progresser la course aux décimales qui devient un sport en vogue et les records ne quittent plus
l’occident...
était d’une nature encore plus complexe, mais on tentait tout de même de
l’exprimer en fonction de nombres simples. Pendant ce temps, la numérotation décimale fait vite
progresser la course aux décimales qui devient un sport en vogue et les records ne quittent plus
l’occident...
Poussant le calcul plus loin qu’Archimède, le record en la matière appartient à Ludolph Van Ceulen
(1539-1610), qui exhiba 20 décimales en 1596 à l’aide de polygones à 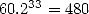 milliards de côtés, puis 32
décimales à l’aide de polygones à
milliards de côtés, puis 32
décimales à l’aide de polygones à 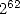 côtés dans une publication posthume de 1615, pour enfin se voir
attribuer et graver sur sa pierre tombale 35 décimales en 1621. Quelle obstination ! Autant dire qu’il passa sa
vie à cet exercice, avec pour récompense que
côtés dans une publication posthume de 1615, pour enfin se voir
attribuer et graver sur sa pierre tombale 35 décimales en 1621. Quelle obstination ! Autant dire qu’il passa sa
vie à cet exercice, avec pour récompense que 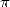 est appelé le nombre de von Ceulen en Allemagne
!
est appelé le nombre de von Ceulen en Allemagne
!
 |
| Ludolph Van-Ceulen (1540-1610) |
En fait il n’y eut guère de progrès réel pendant cette période essentiellement à cause de l’utilisation
exclusive de l’approche géométrique, qui trouvait là ses limites dans le calcul des décimales de
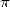 .
.
La quadrature du cercle continue, elle, à poser de véritables problèmes... Sortant de l’ère géométrique qui
n’en a pas donné de solutions, l’analyse va s’y pencher, et on le verra, avec succès. Notons que l’Académie
des Sciences en France, ayant promis une récompense pour la solution, reçoit à cette époque
plusieurs dizaines de preuves erronées. Comme le dit "Le petit Archimède", la palme revient
dans ce domaine à un nommé Liger qui commmençait par démontrer que 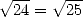 , le reste
suit...
, le reste
suit...
2 Ah enfin l’analyse ! (XVIIIe siècle - fin XIXe siècle)
Le grand tournant eut lieu avec la manipulation de plus en plus courante de sommes et de produits infinis dans le monde mathématique de la fin du moyen-âge.
2.1 Le temps des querelles
A cette époque, de violentes querelles apparaissent: une des plus célèbres concerne Leibniz (1646-1716) et
Newton (1642-1727) qui se disputent la paternité de la découverte du calcul différentiel et perdent beaucoup
d’énergie... Il n’en reste pas moins que malgré le scepticisme de certains (Rolle, par exemple, qui ne croit pas
en cette révolution et va se fâcher avec Varignon, mais n’en fournit pas moins un des théorèmes les plus
célèbres de cette théorie), le calcul différentiel va bouleverser les mathématiques... Les résultats
apparaissent rapidement et la recherche sur 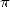 va en bénéficier comme aucune autre. C’est la première
fois que des formules ne traduisent plus directement le lien entre la géométrie par laquelle on
définit
va en bénéficier comme aucune autre. C’est la première
fois que des formules ne traduisent plus directement le lien entre la géométrie par laquelle on
définit 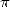 et
et 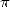 lui-même. C’est d’ailleurs une des choses qui à mon avis fascinent le plus dans
l’étude de
lui-même. C’est d’ailleurs une des choses qui à mon avis fascinent le plus dans
l’étude de 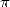 . On a affaire à de grosses formules dans lesquelles il est bien difficile de reconnaître
une propriété géométrique, et pourtant on obtient
. On a affaire à de grosses formules dans lesquelles il est bien difficile de reconnaître
une propriété géométrique, et pourtant on obtient 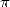 . Et la prime à la recherche d’une solution
concernant le fameux problème de la quadrature du cercle offerte par l’académie des Sciences
engendre un intérêt toujours grand sur la géométrie. Mais tout cela ne s’est pas fait en un jour
:
. Et la prime à la recherche d’une solution
concernant le fameux problème de la quadrature du cercle offerte par l’académie des Sciences
engendre un intérêt toujours grand sur la géométrie. Mais tout cela ne s’est pas fait en un jour
:
2.2 Le prémices de l’analyse
Si il y a un mathématicien qui symbolise un peu ce passage de la géométrie à l’infinitésimal ou à la conscience de l’infini, c’est Wallis (1616-1703).
 |  |
| Wallis (1616-1703) | Lord Brouncker (1620-1684) |
Ses manipulations de suites infinies et ses recherches sur l’aire d’un quart de cercle (en partant de
l’intégrale de 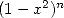 pour arriver à
pour arriver à 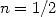 ) le poussent vers des horizons encore inconnus jusqu’alors.
Après une démonstration restée célèbre en raison de ses méandres, il trouve ainsi une très belle formule, le
premier produit infini de rationnels convergeant vers Pi :
) le poussent vers des horizons encore inconnus jusqu’alors.
Après une démonstration restée célèbre en raison de ses méandres, il trouve ainsi une très belle formule, le
premier produit infini de rationnels convergeant vers Pi :
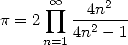 | (6) |
La convergence est éxécrable, mais c’est peut-être la première véritable suite convergeant vers 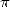 sortie de
l’analyse. Lui succède alors Lord Brouncker (1620-1684), un ami de Wallis, qui, sur sa demande, continue les
recherches vers les fractions continues et transforme le résultat de Wallis en un célèbre développement de
sortie de
l’analyse. Lui succède alors Lord Brouncker (1620-1684), un ami de Wallis, qui, sur sa demande, continue les
recherches vers les fractions continues et transforme le résultat de Wallis en un célèbre développement de 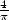 qui donne :
qui donne :
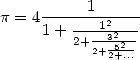 | (7) |
Tout cela tourne beaucoup autour de l’infinitésimal mais ce n’est qu’avec le calcul différentiel que vont vraiment s’épanouir ces techniques.
2.3 Les premières séries
Bien avant les européens, on attribue aux indiens les premières expressions de 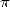 sous forme de série puisque
l’on trouve déjà dans les écrits en sanscrit des disciples de Nilakantha Somayaji (1444 - 1545 !) la
formule
sous forme de série puisque
l’on trouve déjà dans les écrits en sanscrit des disciples de Nilakantha Somayaji (1444 - 1545 !) la
formule
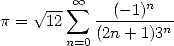 | (8) |
parmi huit autres. Sa simplicité et sa rapidité de convergence (environ 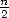 décimales correctes pour
décimales correctes pour 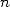 termes) aurait déjà pu mener les mathématiciens de cette époque à connaitre des dizaines de décimales de
termes) aurait déjà pu mener les mathématiciens de cette époque à connaitre des dizaines de décimales de 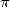 ! Pourtant, à cette époque, comme on l’a vu plus haut, c’est Al Kashi de Samarkande qui vient de réussir le
tour de force de calculer 14 décimales de
! Pourtant, à cette époque, comme on l’a vu plus haut, c’est Al Kashi de Samarkande qui vient de réussir le
tour de force de calculer 14 décimales de 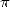 en 1429 à l’aide d’une variante de la méthode d’Archimède et en
système sexagésimal.
en 1429 à l’aide d’une variante de la méthode d’Archimède et en
système sexagésimal.
En Europe, c’est la guerre ! Newton et ses fluxions contre Leibniz et ses 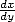 ... L’un comme l’autre ont
au moins le mérite d’avoir eu la vision d’un des bouleversement des mathématiques. L’application du calcul
différentiel permet enfin d’obtenir ou justifier les développements limités en série infinie des fonctions
usuelles (via par exemple la célèbre formule de Taylor). A cette époque, James Gregory (1638-1675)
fait ainsi profiter l’Europe de la découverte du développement en série entière de la fonction
arctan
... L’un comme l’autre ont
au moins le mérite d’avoir eu la vision d’un des bouleversement des mathématiques. L’application du calcul
différentiel permet enfin d’obtenir ou justifier les développements limités en série infinie des fonctions
usuelles (via par exemple la célèbre formule de Taylor). A cette époque, James Gregory (1638-1675)
fait ainsi profiter l’Europe de la découverte du développement en série entière de la fonction
arctan
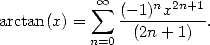 | (9) |
L’application de 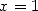 donne immédiatement une série pour Pi, mais, bizarrement, Gregory passe à côté
(ou plus probablement, n’y voit pas d’intérêt) et celle-ci ne se retrouve que dans l’oeuvre de Leibniz. En 1671,
c’est Abraham Sharp (1651-1742) qui utilise le cas particulier
donne immédiatement une série pour Pi, mais, bizarrement, Gregory passe à côté
(ou plus probablement, n’y voit pas d’intérêt) et celle-ci ne se retrouve que dans l’oeuvre de Leibniz. En 1671,
c’est Abraham Sharp (1651-1742) qui utilise le cas particulier 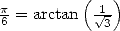 , autrement dit l’équation 8,
pour obtenir 71 décimales correctes de
, autrement dit l’équation 8,
pour obtenir 71 décimales correctes de 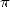 en 1699, près de 200 ans après Nilakantha ! Le développement
d’arcsin fut obtenu par Newton vers 1665-1666, qui en profita pour calculer 15 décimales de
en 1699, près de 200 ans après Nilakantha ! Le développement
d’arcsin fut obtenu par Newton vers 1665-1666, qui en profita pour calculer 15 décimales de 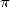 , n’ayant “rien
d’autre à faire” comme il l’affirma lui-même.
, n’ayant “rien
d’autre à faire” comme il l’affirma lui-même.
 |
| Newton (1642-1727) |
La fonction arctan est un bon candidat pour le calcul des décimales de 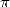 à la main car si l’on s’y prend
bien, on n’utilise que des termes rationnels ou au plus une racine comme dans 8. Ainsi John
Machin (1680-1752) parvient aisément à 100 décimales en 1706 en proposant la désormais célèbre
formule
à la main car si l’on s’y prend
bien, on n’utilise que des termes rationnels ou au plus une racine comme dans 8. Ainsi John
Machin (1680-1752) parvient aisément à 100 décimales en 1706 en proposant la désormais célèbre
formule
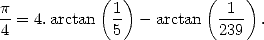 | (10) |
 |
| John Machin (1680-1752) |
La démonstration ou la recherche de ce type de formules (dont quatre autres exemples sont donnés plus loin par les équations 12, 13, 23 et 24) s’obtient grâce à la règle suivante
Theorem 2.1 Soient 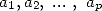 et
et 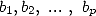 des entiers.
des entiers. 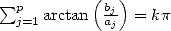 ,
,
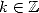 , si et seulement si
, si et seulement si 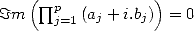 .
.
Proof. Si 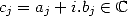 ,
, ![( prod p ) sum p
ln j=1 (aj + i.bj) = j=1 [ln(| cj|)+ i.(arg(cj)+ 2kjp)]](../histoire/histoire110x.gif)
![sum p [ ( (bj) )]
= j=1 ln(|cj|)+ i. arctan aj + 2kjp](../histoire/histoire111x.gif) ,
,
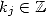 . En conséquence
. En conséquence 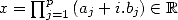 ssi
ssi 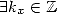 tel que
tel que 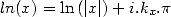 , ssi
, ssi
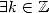 tel que
tel que 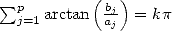 .
__
.
__
La rapidité de convergence de ces formules est contrainte par le plus grand terme 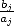 et d’après l’eq. 9, on
obtient une convergence linéaire, autrement dit un nombre
et d’après l’eq. 9, on
obtient une convergence linéaire, autrement dit un nombre 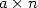 de décimales en utilisant
de décimales en utilisant 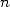 termes du
développement de Taylor de la fonction
termes du
développement de Taylor de la fonction 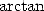 . Désormais, les combinaisons d’arctan vont servir de base à la
course aux décimales jusqu’en 1985 !
. Désormais, les combinaisons d’arctan vont servir de base à la
course aux décimales jusqu’en 1985 !
2.4 Le seigneur des séries
Après que la prédominance mathématique se soit installée en Angleterre sous l’impulsion de Newton, celle-ci revient sur le vieux continent, en Suisse notamment avec les Bernoulli et Euler. C’est la grande époque de l’analyse. Euler fouille partout et défriche inlassablement pour nous fournir d’innombrables formules. La plus belle est certainement :
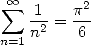
qui n’apporte guère au calcul des décimales mais dont la simplicité est tout à fait remarquable.... Sa démonstration (voir page Euler) est un modèle du genre, absolument pas rigoureuse, mais tout à fait géniale !
 |
| Euler (1707-1783) |
Un siècle plus tard, un des mathématiciens qui selon moi va indirectement apporter le plus à la recherche
sur 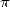 est Joseph Fourier (1768-1830). Sa théorie sur la décomposition d’une fonction périodique en série,
encore à finaliser mais qui va faire l’objet d’un passage à la rigueur tout au long du XIXe siècle, est
véritablement révolutionnaire (tant d’ailleurs que certains mathématiciens de l’époque comme Poisson
s’élèveront contre avec beaucoup d’énergie !). Ce résultat permet en effet de redémontrer simplement à
peu près toutes les formules de ce bon vieux Euler. Et bien sûr d’en trouver de nouvelles assez
intéressantes.
est Joseph Fourier (1768-1830). Sa théorie sur la décomposition d’une fonction périodique en série,
encore à finaliser mais qui va faire l’objet d’un passage à la rigueur tout au long du XIXe siècle, est
véritablement révolutionnaire (tant d’ailleurs que certains mathématiciens de l’époque comme Poisson
s’élèveront contre avec beaucoup d’énergie !). Ce résultat permet en effet de redémontrer simplement à
peu près toutes les formules de ce bon vieux Euler. Et bien sûr d’en trouver de nouvelles assez
intéressantes.
2.5  , probablement...
, probablement...
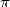 , ce n’est pas seulement la géométrie et l’analyse ! Buffon (1707-1788) nous prouve avec son célèbre
problème de l’aiguille que
, ce n’est pas seulement la géométrie et l’analyse ! Buffon (1707-1788) nous prouve avec son célèbre
problème de l’aiguille que 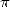 intervient aussi dans le domaine des probabilités. Bien sûr, ce résultat est
toujours dû à la définition de
intervient aussi dans le domaine des probabilités. Bien sûr, ce résultat est
toujours dû à la définition de 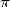 comme composante de l’aire et du périmètre du cercle, mais le théorème de
Cesàro (1859 - 1906) confirmera l’incursion de
comme composante de l’aire et du périmètre du cercle, mais le théorème de
Cesàro (1859 - 1906) confirmera l’incursion de 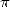 dans les probabilités...
dans les probabilités...
 |  |
| Buffon (1707-1788) | Cesàro (1859-1906) |
2.6 Le défi
Revenons à notre course chronologique. À partir de Newton, ce sont - sans leur faire injure -
plutôt des mathématiciens de second plan qui se battent pour le record de décimales. D’ailleurs,
le nombre de décimales déjà calculé en ces temps est bien supérieur aux véritables besoins des
mathématiciens et des physiciens. On estime en effet que pour calculer la circonférence de l’univers avec la
précision d’un atome d’hydrogène, seules 39 décimales de 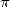 sont requises ! Les motivations
sont donc plutôt tournées vers la recherche de périodicités ou motifs dans les décimales de
sont requises ! Les motivations
sont donc plutôt tournées vers la recherche de périodicités ou motifs dans les décimales de 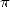 .
La périodicité des décimales d’un nombre en fait un rationnel (nombre s’écrivant comme une
fraction
.
La périodicité des décimales d’un nombre en fait un rationnel (nombre s’écrivant comme une
fraction 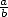 ,
,  ,
, 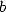 entiers). Pourtant, à l’aube du XVIIIe et du XIXe siècle, le problème de
l’irrationnalité de
entiers). Pourtant, à l’aube du XVIIIe et du XIXe siècle, le problème de
l’irrationnalité de 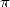 , autrement dit l’impossibilité d’écrire
, autrement dit l’impossibilité d’écrire 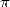 sous la forme d’un rationnelle,
tracasse toujours les mathématiciens. Ils la soupçonnent vraie depuis longtemps mais n’avaient
jamais réussi à la prouver. Avec les progrès de l’analyse, Euler montre celle de
sous la forme d’un rationnelle,
tracasse toujours les mathématiciens. Ils la soupçonnent vraie depuis longtemps mais n’avaient
jamais réussi à la prouver. Avec les progrès de l’analyse, Euler montre celle de  et Johann
Lambert (1728-1777) apporte une réponse au problème pour
et Johann
Lambert (1728-1777) apporte une réponse au problème pour 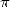 en 1761. Sa démonstration plutôt lourde
s’appuie sur un développement en fraction continue de la fonction
en 1761. Sa démonstration plutôt lourde
s’appuie sur un développement en fraction continue de la fonction 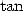 . Pi est bien irrationnel
!
. Pi est bien irrationnel
!
 |
| Lambert (1728-1777) |
Voilà en fait le résultat peut-être paradoxalement le plus important que l’on ait trouvé sur la répartition des décimales de Pi tant cette dernière demeure un mystère encore de nos jours. L’irrationnalité indique ainsi qu’elles ne sont pas périodiques...
Restait la transcendance, autrement dit l’impossibilité de représenter 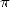 comme une combinaison de
racines et de puissances d’entiers, ou en terme équivalents, le fait que
comme une combinaison de
racines et de puissances d’entiers, ou en terme équivalents, le fait que 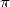 ne soit racine d’aucun polynome à
coefficients entiers, ou bien encore l’impossibilité de la quadrature du cercle. Malgré les efforts de beaucoup de
mathématiciens (et amateurs qui cherchent toujours à résoudre la quadrature du cercle !), cette citadelle reste
imprenable jusqu’à la fin du XIXe siècle. Et les délires des mathématiciens amateurs obligent de plus
l’académie des Sciences à refuser à partir de 1775 les tentatives de démonstration de la quadrature du cercle,
conséquence immédiate de la transcendance.
ne soit racine d’aucun polynome à
coefficients entiers, ou bien encore l’impossibilité de la quadrature du cercle. Malgré les efforts de beaucoup de
mathématiciens (et amateurs qui cherchent toujours à résoudre la quadrature du cercle !), cette citadelle reste
imprenable jusqu’à la fin du XIXe siècle. Et les délires des mathématiciens amateurs obligent de plus
l’académie des Sciences à refuser à partir de 1775 les tentatives de démonstration de la quadrature du cercle,
conséquence immédiate de la transcendance.
2.7 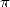 tombe dans l’ombre
tombe dans l’ombre
Le XIXe siècle arrive... Bizarrement, le plus brillant représentant du génie scientifique de ce siècle, Maître
Gauss (1777-1855), malgré son talent incomparable, n’est pas celui qui s’intéressera le plus à la recherche sur
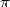 , au moins pas directement. On lui doit quelques petites formule d’arctan, mais pas de quoi se rouler par
terre !
, au moins pas directement. On lui doit quelques petites formule d’arctan, mais pas de quoi se rouler par
terre !
Bien que Pi continue à apparaître dans de nombreux résultats, le XIXe siècle se tourne plutôt vers
l’algèbre et l’arithmétique avec Galois, Abel, Sophie Germain et les tout nouveaux théoriciens de la géométrie
non euclidienne tels Gauss, Beltrami, Lobatchevski et Bolyai. Le calcul des décimales semble aussi s’essoufler
après la deuxième moitié du XIXe siècle. Tout cela malgré le talent extraordinaire de Zacharias Dase,
et l’ardeur de quelques passionnés comme Shanks. Employé par Strassnitsky pour calculer 200
décimales, ce qu’il fit en deux mois, Dase était l’annonciateur des ordinateurs modernes par ses
fantastiques capacités de calcul (il pouvait multiplier de tête deux nombres de 100 chiffres en
8h, en faisant des pauses, ou bien dormant une nuit entière, et reprenant plus tard !) . Il faut
dire que les limites humaines de calcul des décimales à la main semblent atteintes en 1874 avec
l’obtention de 707 décimales par Shanks, qui sont d’ailleurs fausses à partir de la 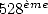 . Ferguson le
remarquera près de 70 ans plus tard en les comparant aux
. Ferguson le
remarquera près de 70 ans plus tard en les comparant aux 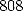 qu’il obtint en 1948, avec les
premières machines à calculer (des additionneurs en fait, hérités du principe de celle construite par
Leibniz dès 1694). Une erreur qui aura donc durée 92 ans ! La salle du palais de la découverte
à Paris qui arborait fièrement le résultat de Shanks en fut quitte pour une rapide rénovation
!
qu’il obtint en 1948, avec les
premières machines à calculer (des additionneurs en fait, hérités du principe de celle construite par
Leibniz dès 1694). Une erreur qui aura donc durée 92 ans ! La salle du palais de la découverte
à Paris qui arborait fièrement le résultat de Shanks en fut quitte pour une rapide rénovation
!
 |
| La salle consacée aux mathématiques du Palais de la Découverte à Paris. |
Et depuis les formules d’arctan, on n’a toujours pas trouvé à cette époque un moyen d’aller plus vite et plus loin en théorie comme en pratique...
De plus, le plus vieux problème mathématique se trouve résolu par Lindemann en 1882 lorsqu’il démontre
la transcendance de 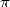 . La quadrature du cercle est donc impossible... Comment va-t-on sortir de cette
impasse et se remotiver ?
. La quadrature du cercle est donc impossible... Comment va-t-on sortir de cette
impasse et se remotiver ?
C’est qu’au fin fond de l’Inde grandit en cette fin de XIXe siècle un personnage qui va tout bouleverser et révolutionner le siècle à venir... L’ère des algorithmes et de l’informatique va commencer avec lui...
3 L’ordinateur prend le relais
3.1 Le souffle Indien
Durant la première moitié du XXe siècle, les préoccupations mathématiques sont encore ailleurs. Les théories élaborées par Cantor, Gödel, Kolmogorov, la topologie et la liste des 23 problèmes de Hilbert ouvrent tout à coup des horizons qui donnent un coup de vieux à l’analyse classique. Celle-ci semblait pourtant avait trouvé son évolution naturelle dans l’étude des intégrales elliptiques menées par Legendre, puis Gauss, Abel et Jacobi durant la première moitié du XIXe siècle.
Heureusement un génie né au fin fond de l’Inde en 1887, Srinivasa Ramanujan (fig. ??), va se charger de
donner un souffle nouveau aux recherches menées autour de 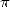 .
.
 |
| Srinivasa Ramanujan (1887 - 1920). |
Lui-même passionné par cette constante, c’est un autodidacte complet qui passa les 25 premières années de sa vie à reconstruire les mathématiques à partir d’un unique ouvrage de 6165 théorèmes sans démonstration (“Synopsis of elementary results in pure and applied mathematics” de G.S.Carr). Cet état d’esprit le conduisit à énoncer la plupart de ses résultats sans démonstration (ce qui ne signifie pas qu’il ne comprenait pas d’où ils venaient !). Doté d’une intuition exceptionnelle qui lui permit de progresser à pas de géants dans la théorie des nombres et des équations modulaires, il découvrit des formules venues d’ailleurs comme celle-ci publiée en 1914
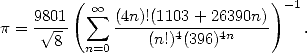 | (11) |
Il existe une anecdote célèbre à propos de cette formule : sa démonstration presque entière fut achevée au début des années 80 par les frères Borwein [7].
 |  |
| Frères Borwein
| |
Il restait le coefficient 1103 à justifier, il devait être entier, mais la longueur des calculs et équations
requises était épouvantable. Gosper effectua alors en 1985 un calcul “à l’aveugle” de 17 millions de décimales
de 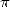 à l’aide de cette formule. Aussi vrai que deux entiers proches de moins d’une unité sont égaux, la
concordance des résultats du calcul de Gosper avec les 10 millions de décimales déjà connues à l’époque
constitua une démonstration finale de la formule de Ramanujan ! On suppose que Ramanujan avait du
procéder de même sur quelques décimales.
à l’aide de cette formule. Aussi vrai que deux entiers proches de moins d’une unité sont égaux, la
concordance des résultats du calcul de Gosper avec les 10 millions de décimales déjà connues à l’époque
constitua une démonstration finale de la formule de Ramanujan ! On suppose que Ramanujan avait du
procéder de même sur quelques décimales.
Les Borwein tireront des travaux de Ramanujan une ribambelle d’algorithmes remarquables assez
largement utilisés de nos jours dans le calcul des décimales de 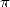 (voir paragraphe 3.5). La complexité de la
démonstration d’une telle formule est telle que malheureusement même un survol des résultats, sans
démonstration des intermédiaires, occupe au minimum une dizaine de pages dans le remarquable ouvrage [13].
Le lecteur intéressé par une plongée dans l’univers passionnant des équations modulaires, corps
quadratiques, et autres intégrales elliptiques pourra se référer à la ”Bible” [7], d’une pédagogie
remarquable.
(voir paragraphe 3.5). La complexité de la
démonstration d’une telle formule est telle que malheureusement même un survol des résultats, sans
démonstration des intermédiaires, occupe au minimum une dizaine de pages dans le remarquable ouvrage [13].
Le lecteur intéressé par une plongée dans l’univers passionnant des équations modulaires, corps
quadratiques, et autres intégrales elliptiques pourra se référer à la ”Bible” [7], d’une pédagogie
remarquable.
Ramanujan fut repéré par le mathématicien anglais Hardy auquel il avait écrit une lettre en 1913, s’embarqua pour l’Angleterre en 1914 et leur collaboration fructueuse dura jusqu’en 1919.
 |
| Hardy (1877-1947) |
Il repartit alors en Inde où il mourut l’année suivante, probablement de carences en vitamines. Considéré comme un des plus grands génies du XXe siècle, Ramanujan a laissé des carnets remplis de formules en notations non-standards, dont le déchiffrage s’est poursuivi jusqu’à nos jours (!), d’abord assuré par Bruce Berndt, puis par les frères Borwein.
3.2 La course aux décimales reprend
Après Ramanujan qui meurt prématurément en 1920, c’est le désert théorique... jusqu’en 1976. Donc, pendant ce temps, on calcule... Après la guerre, l’avènement des machines à calculer fait progresser la course aux décimales à pas de géants ! Ferguson ouvre le bal en 1946 en obtenant 620 décimales à l’aide d’un calculateur de bureau. Le premier calcul sur ordinateur est confié au fameux ENIAC en 1949 qui rend 2037 décimales en 70 heures à l’aide de la formule de Machin 10.
 |
| L’ENIAC |
En 1973, Guilloud et Bouyer atteignent le premier million de décimales sur CDC 7600 à l’aide de deux
formules d’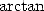 célèbres, celles de Gauss 12 et de Störmer 13
célèbres, celles de Gauss 12 et de Störmer 13
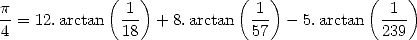 | (12) |
 | (13) |
Le calcul en binaire prit respectivement 22h11 et 13h40, et la conversion en base décimale 1h07. Un livre de 415 pages de décimales tiré de ce calcul fut qualifié à l’époque de “livre le plus ennuyeux du monde” !
Il faut noter que le processus attaché à la course aux décimales est toujours le même jusqu’à aujourd’hui :
les calculs sont effectués avec deux formules distinctes puis comparés pour validation du record.
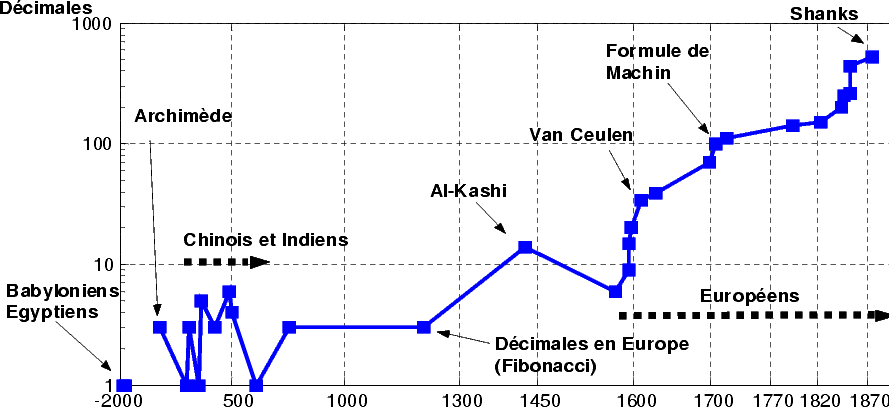
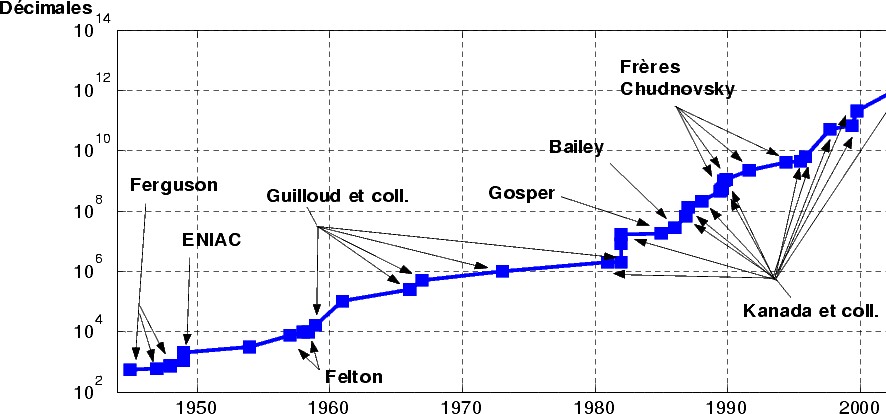
Les figures 1 et 2 montrent l’évolution des records de calcul de décimales de 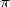 au cours des
siècles.
au cours des
siècles.
|
|
3.3 Zorro est arrivééé : améliorations algorithmiques
A cette époque, le manque d’algorithme de multiplication efficace oblige à segmenter chaque
nombre en tranches, par exemple 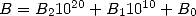 . La multiplication de nombres de
taille
. La multiplication de nombres de
taille 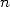 nécessite alors un temps (ou nombre d’opérations) proportionnel à
nécessite alors un temps (ou nombre d’opérations) proportionnel à 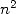 sans compter
l’utilisation mémoire proportionnelle à
sans compter
l’utilisation mémoire proportionnelle à 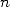 . Sans des améliorations théoriques et algorithmiques, la
progression du record de décimales aurait donc été très lente. C’est alors à cette époque que les choses
s’accélèrent.
. Sans des améliorations théoriques et algorithmiques, la
progression du record de décimales aurait donc été très lente. C’est alors à cette époque que les choses
s’accélèrent.
En 1965, Cooley et Tukey introduisent sous sa forme moderne une méthode de réduction de la
complexité du calcul des séries de Fourier connue aujourd’hui sous le nom de Transformée de
Fourier Rapide [11]. Schönhage et Strassen en tirent un algorithme de multiplication de grands
entiers en compexité 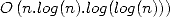 ce qui est considérablement mieux que
ce qui est considérablement mieux que 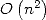 [24]
!
[24]
!
En 1976, Salamin et Brent parviennent indépendamment au même algorithme ([23, 8])
qui a une propriété extraordinaire de convergence quadratique, autrement dit le nombre de décimales
exactes double à chaque itération. En effet, Salamin montre dans [23] que si 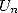 est l’approximation de
est l’approximation de  après
après 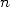 itérations de l’algorithme 14, on a
itérations de l’algorithme 14, on a
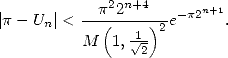 | (16) |
Cette majoration montre que le nombre de décimales correctes de 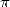 obtenues à partir de
obtenues à partir de 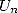 est
strictement supérieur à
est
strictement supérieur à  .
. 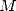 désigne ici la moyenne
arithmético géométrique (voir page Salamin).
désigne ici la moyenne
arithmético géométrique (voir page Salamin).
 |
| Richard Brent |
Ajoutons enfin que l’algorithme de Newton, proposé vers 1669 (!), ramène la division et l’extraction de racines carrées à des multiplications et propose une convergence elle aussi quadratique. Autant dire que tous les ingrédients sont réunis pour faire exploser les records !
3.4 Compèt’ sur la planète
La compétition reprend en effet en 1981 avec l’équipe de Kanada qui fut probablement la première à appliquer
ce cocktail d’algorithmes (FFT , Newton, Brent-Salamin). Myioshi et Kanada obtiennent 2 000 036
décimales en 1981. À partir de ce moment, le rythme s’accélère franchement, puisque le pauvre
Guilloud, qui tente de garder son record en 1982 en calculant 14 décimales de plus que le couple
japonais, se trouve hors du coup à la fin de l’année 1982, où l’on connait 16 777 206 décimales
(Kanada, Yochino et Tamura). La lutte concernera ensuite principalement Kanada et, entre 1991
et 1994, les deux frères David et Gregory Chudnovsky qui utiliseront une série de leur cru de
type Ramanujan et un ordinateur dont ils ont eux-même conçu l’architecture. Selon la légende,
leur appartement New-Yorkais contient des montagnes de papiers en désordre et est chauffé aux
microprocesseurs ! Ces mathématiciens isolés mais au talent reconnu (Gregory est considéré comme un génie
exceptionnel mais il est atteint d’une maladie l’empêchant de travailler en université) montrent
au moins que des scientifiques de tout premier plan s’intéressent au calcul des décimales de 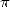 [12].
[12].
3.5 Une avalanche de formules
Les années 80 voient l’éclosion de plusieurs formules très intéressantes concernant 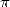 . Il y a les
formules de type Ramanujan, des séries infinies convergeant linéairement mais assez rapidement
pour qu’elles soient utilisées dans les records. Celles-ci sont retrouvées et expliquées grâce au
décryptage des carnets de Ramanujan par Bruce Berndt et aux travaux des frères Borwein et
Chudnovsky.
. Il y a les
formules de type Ramanujan, des séries infinies convergeant linéairement mais assez rapidement
pour qu’elles soient utilisées dans les records. Celles-ci sont retrouvées et expliquées grâce au
décryptage des carnets de Ramanujan par Bruce Berndt et aux travaux des frères Borwein et
Chudnovsky.
D’autre part, à partir d’équations modulaires impliquant les thêta fonctions (dont l’algorithme de Brent-Salamin est un cas particulier), les frères Borwein ont montré que l’on pouvait construire des algorithmes convergeant à n’importe quelle vitesse (quadratique, quartique, quintique...) vers Pi même si la complexité des calculs augmente en conséquence. Un bon compromis semble être la formule suivante, à convergence quartique [7] :
Elle fut utilisée pour la première fois par Baileypuis Kanada en 1986. Bailey utilisa 12 itérations sur un
CRAY-2 pour calculer 29 360 000 décimales de 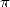 (en fait 45 millions sont possibles à cette étape). Il est
amusant de constater qu’il suffit alors de moins de 100 multiplications, divisions et extractions de racines pour
y parvenir !
(en fait 45 millions sont possibles à cette étape). Il est
amusant de constater qu’il suffit alors de moins de 100 multiplications, divisions et extractions de racines pour
y parvenir !
De 1982 à 2002, ce sont toujours des formules de Ramanujan (comme 11), l’algorithme de
Brent-Salamin (14) ou une variante, ainsi que l’algorithme quartique des Borwein (17) qui
ont été utilisés dans la course au record de calcul de décimales de 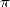 . Le premier milliard est
atteint par les frères Chudnovsky en 1989 et, avec cette méthode, Kanada, toujours lui, atteint
206 milliards de décimales de
. Le premier milliard est
atteint par les frères Chudnovsky en 1989 et, avec cette méthode, Kanada, toujours lui, atteint
206 milliards de décimales de 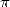 en 1999. Bien sûr, Pi ayant un nombre infini de décimales, ce
n’est même pas une goutte d’eau, mais les mathématiciens espèrent toujours remarquer, comme
les frères Chudnovsky , quelque irrégularité ou propriété dans les décimales de notre constante
favorite...
en 1999. Bien sûr, Pi ayant un nombre infini de décimales, ce
n’est même pas une goutte d’eau, mais les mathématiciens espèrent toujours remarquer, comme
les frères Chudnovsky , quelque irrégularité ou propriété dans les décimales de notre constante
favorite...
 |
| Frères Chudnovsky |
 |
De gauche à droite, Salamin, Kanada, Bailey et Gosper en 87. Ah, les soirées délirantes entre potes sur  ! ! |
4 L’approche BBP, encore du nouveau sur 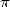
4.1 Comment progresser ?
La multiplication, la division et l’extraction de racine s’effectuant désormais dans un temps quasi-linéaire, et
sachant que l’on ne peut pas descendre en dessous d’une complexité 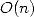 , il ne faut plus guère attendre
d’avancées significatives de ce côté. Nous avons vu que des algorithmes extrêmement efficaces existaient pour
le calcul des décimales de
, il ne faut plus guère attendre
d’avancées significatives de ce côté. Nous avons vu que des algorithmes extrêmement efficaces existaient pour
le calcul des décimales de 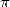 . Alors est-on condamné à voir les records tomber en fonction de la progression
des performances des ordinateurs ? Oui et non !
. Alors est-on condamné à voir les records tomber en fonction de la progression
des performances des ordinateurs ? Oui et non !
Les mathématiques surprennent souvent là où on ne les attend plus. C’est ainsi que le 19 septembre 1995 à 0h29 (!), après des mois de recherches à tâtons, Simon Plouffe, David Bailey et Peter Borwein de Vancouver découvrent la formule apparemment simple et anodine
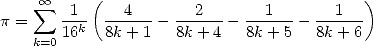 | (18) |
appelée depuis formule BBP. La démonstration en est presque immédiate en remarquant que
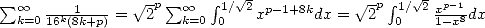 puis en calculant l’intégrale équivalente
à 18. Euler aurait lui-même pu la découvrir. En fait, c’est à ce jour un des plus célèbres exemples de
mathématiques expérimentales puisque cette formule fut découverte par l’algorithme PSLQ de recherche de
relations linéaires entre nombres. Ceci encouragea nombre d’amateurs en mathématiques à se lancer dans la
recherche de telles formules grâce à PSLQ ou LLL, un algorithme similaire implémenté dans le logiciel
Pari-GP.
puis en calculant l’intégrale équivalente
à 18. Euler aurait lui-même pu la découvrir. En fait, c’est à ce jour un des plus célèbres exemples de
mathématiques expérimentales puisque cette formule fut découverte par l’algorithme PSLQ de recherche de
relations linéaires entre nombres. Ceci encouragea nombre d’amateurs en mathématiques à se lancer dans la
recherche de telles formules grâce à PSLQ ou LLL, un algorithme similaire implémenté dans le logiciel
Pari-GP.
 |
| Simon Plouffe |
Mais nos trois mathématiciens canadiens remarquent surtout que cette expression est très proche d’une
décomposition en base 16 de 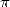 . Dans l’article [3] de 1996 devenu célèbre, ils montrent que l’on peut se servir
de 18 pour atteindre le
. Dans l’article [3] de 1996 devenu célèbre, ils montrent que l’on peut se servir
de 18 pour atteindre le 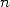 -ième digit de
-ième digit de 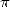 en base
en base 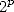 (a fortiori en base 16) sans avoir calculé les
précédents, ceci en temps presque linéaire
(a fortiori en base 16) sans avoir calculé les
précédents, ceci en temps presque linéaire 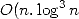 ) et en espace
) et en espace 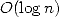 !! L’espace requis étant
minime, ils appliquent immédiatement ce résultat en calculant le
!! L’espace requis étant
minime, ils appliquent immédiatement ce résultat en calculant le 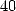 milliardième digit de
milliardième digit de 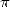 en base 2. La
révolution est en marche.
en base 2. La
révolution est en marche.
Plouffe étend ce résultat à toutes les bases 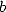 en octobre 1996 [22] au prix d’un temps
en octobre 1996 [22] au prix d’un temps 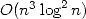 et
de l’utilisation astucieuse de la série
et
de l’utilisation astucieuse de la série
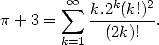 | (19) |
Des améliorations en 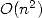 puis en
puis en 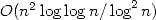 sont successivement proposées par Bellard en
1997 [5] puis Gourdon en 2003 [14]. De nombreuses autres formules type BBP ( avec des puissances de
sont successivement proposées par Bellard en
1997 [5] puis Gourdon en 2003 [14]. De nombreuses autres formules type BBP ( avec des puissances de
 ou
ou 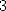 ) ont depuis vu le jour pour les logarithmes d’entiers,
) ont depuis vu le jour pour les logarithmes d’entiers, 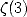 ,
, 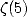 , la constante de
Catalan
, la constante de
Catalan 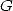 , et de manière générale les constantes polylogarithmiques [9, 17]. Par contre, il n’existe
probablement pas de formule pour
, et de manière générale les constantes polylogarithmiques [9, 17]. Par contre, il n’existe
probablement pas de formule pour 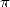 avec une puissance de
avec une puissance de 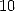 , autrement dit en base
, autrement dit en base 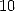 . La formule
. La formule
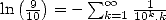 montre cependant que l’on peut calculer isolément les chiffres décimaux de certaines
constantes.
montre cependant que l’on peut calculer isolément les chiffres décimaux de certaines
constantes.
Ces résultats fondamentaux montrent en particulier que 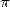 appartient à la classe de complexité de
Steven
appartient à la classe de complexité de
Steven 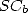 , regroupant les constantes dont on peut calculer les chiffres en base
, regroupant les constantes dont on peut calculer les chiffres en base 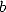 en temps
polynomial et espace
en temps
polynomial et espace 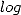 -polynomial, ce qui était auparavant jugé improbable du point de vue
mémoire.
-polynomial, ce qui était auparavant jugé improbable du point de vue
mémoire.
Depuis lors, Fabrice Bellard, un étudiant français Polytechnicien, réussit à atteindre le 1000 milliardième
digit en septembre 1997. Puis Colin Percival a atteint le 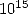 -ème digit binaire de
-ème digit binaire de 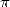 (un
(un  !) au
moyen d’un calcul collaboratif extravagant sur internet de 1.2 millions d’heures CPU partagées
entre 1734 ordinateurs répartis dans 56 pays entre le 5 septembre 1998 et le 11 septembre 2000
!
!) au
moyen d’un calcul collaboratif extravagant sur internet de 1.2 millions d’heures CPU partagées
entre 1734 ordinateurs répartis dans 56 pays entre le 5 septembre 1998 et le 11 septembre 2000
!
Le principe de ce calcul du 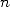 -ième digit de
-ième digit de 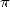 est donné a la page N-ième digit.
est donné a la page N-ième digit.
4.2 Une formule pleine de ressources
L’accès presque direct aux digits de ces constantes a fait naître chez les mathématiciens l’idée que l’on
pourrait trouver des propriétés de répartition de ces digits, et que l’on était peut-être proche d’une preuve de
la normalité de 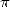 (et donc de l’irrationnalité de la constante de Catalan
(et donc de l’irrationnalité de la constante de Catalan 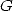 ou des
ou des 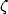 impairs). La
normalité d’un nombre requiert que chaque
impairs). La
normalité d’un nombre requiert que chaque 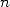 -uplet possible apparaisse avec la probabilité
-uplet possible apparaisse avec la probabilité 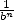 dans les
digits en base
dans les
digits en base 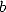 de ce nombre. Genre chaque chiffre entre
de ce nombre. Genre chaque chiffre entre  et
et 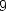 apparaît en moyenne 1 fois sur
apparaît en moyenne 1 fois sur 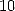 ,
chaque nombre entre
,
chaque nombre entre  et
et 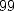 apparaît 1 fois sur
apparaît 1 fois sur 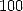 , et ainsi de suite. En octobre 2000,
Bailey et Crandall ont réduit cette condition de normalité à la vérification de l’hypothèse suivante
:
, et ainsi de suite. En octobre 2000,
Bailey et Crandall ont réduit cette condition de normalité à la vérification de l’hypothèse suivante
:
Conjecture 4.1 Soit 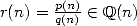 ,
, 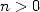 , avec
, avec 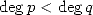 et
et  sans pôles sur
sans pôles sur 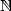 (c’est la
partie polynômiale des formules BBP). Soit une base
(c’est la
partie polynômiale des formules BBP). Soit une base 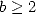 et
et 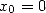 . Alors la suite
. Alors la suite 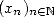 définie
par
définie
par
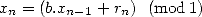 | (20) |
a un attracteur fini ou est équidistribuée sur ![[0,1]](../histoire/histoire235x.gif) .
.
 |
| Richard E. Crandall |
Cette forme de suite est équivalente à la représentation BBP d’une constante puisque si
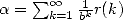 , alors
, alors 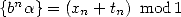 où
où 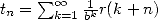 tend vers 0 si
tend vers 0 si 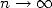 puisque
puisque 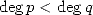 .
.
La condition d’atracteur fini représente intuitivement le fait pour une séquence de d’approcher toujours d’un ensemble de valeurs finies à partir d’un certain rang, et dans n’importe quel ordre, comme si l’on tendait vers un rationnel généralisé (dont les séquences de décimales sont périodiques).
Definition 4.2 Précisément, une suite ![(xn)n (- N (- [0,1]](../histoire/histoire241x.gif) possède un attracteur fini
possède un attracteur fini 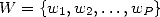 s’il existe
s’il existe 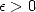 et
et 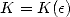 tel que pour tout
tel que pour tout 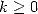 ,
,
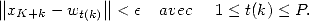 | (21) |
On peut d’ailleurs montrer que dans le cas qui nous intéresse (formules BBP), cette propriété est
équivalente à la rationnalité de la limite de 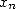 [4]. La notion d’équidistribution est plus intuitive. Elle est
vérifiée si la proportion d’apparition d’une séquence à valeurs dans
[4]. La notion d’équidistribution est plus intuitive. Elle est
vérifiée si la proportion d’apparition d’une séquence à valeurs dans ![[0,1]](../histoire/histoire248x.gif) dans un intervalle donné
dans un intervalle donné ![[c,d]](../histoire/histoire249x.gif) est
justement la longueur de cet intervalle, bref si les valeurs prises sont distribuées uniformément dans
est
justement la longueur de cet intervalle, bref si les valeurs prises sont distribuées uniformément dans ![[0,1]](../histoire/histoire250x.gif) .
.
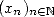 est équidistribuée si
est équidistribuée si
![lim Card-{xj (- -[c,d], j-<-n} = d- c.
n--> oo n](../histoire/histoire252x.gif) | (22) |
L’équidistribution pour ce type de séquences implique la normalité [19]. Compte-tenu de la variété des
constantes impliquées dans des représentations BBP, on touche là à des avancées importantes, notamment
pour les 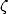 impairs. Il est amusant de voir la simplicité de la formule BBP dont sont tirées toutes ces
conséquences. On consultera [4, 20] pour approfondir ces questions ouvertes.
impairs. Il est amusant de voir la simplicité de la formule BBP dont sont tirées toutes ces
conséquences. On consultera [4, 20] pour approfondir ces questions ouvertes.
5 Une quête sans fin ?
5.1 Record en date
Le 6 décembre 2002. Kanada, compétiteur infatigable qui détient ou reprend le record de calcul de décimales
de 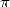 depuis plus de 20 ans, a calculé 1 241 100 000 000 décimales de
depuis plus de 20 ans, a calculé 1 241 100 000 000 décimales de 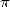 . La surprise est venue du fait qu’il a
utilisé cette fois deux formules de type Machin comme l’eq. 10.
. La surprise est venue du fait qu’il a
utilisé cette fois deux formules de type Machin comme l’eq. 10.
Ce retour à des formules étonnament simples après l’utilisation pendant une quinzaine d’années des algorithmes de Brent-Salamin, des Borwein ou des séries de Ramanujan et Chudnovsky était vraiment inattendu. Il semble que l’utilisation perpétuelle de racines, multiplications et divisions nécessitait l’utilisation de la transformée de Fourier rapide (FFT) à très grande échelle. Cette dernière requiert énormément de mémoire pour fonctionner. Kanada est donc revenu à des méthodes plus sages comme les formules type Machin, qui nécessitent sensiblement plus d’opérations arithmétiques mais moins de FFT et donc beaucoup moins de mémoire. Kanada estime que son implémentation est environ deux fois plus plus rapide que la précédente qui utilisait l’algorithme 14 de Brent-Salamin et celui d’ordre quartique des Borwein (eq. 17). Les calcul ont été effectués en base hexadécimale, soit 1 030 700 000 000 digits. Les formules employées sont :
La première a été trouvée en 1982 par un professeur de mathématiques et compositeur, Takano, et la seconde est une découverte de Störmer en 1896.
Ce calcul de Kanada recèle une seconde originalité : comme le résultat avait été obtenu en base 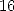 , après
avoir vérifié l’adéquation entre les deux calculs, il a effectué une vérification supplémentaire en
calculant directement les 20 digits hexadécimaux à la position 1 000 000 000 001 à l’aide de
l’approche par formules BBP présentée précédemment. Le résultat B4466E8D21 5388C4E014,
qui a requis 21 heures de travail, a parfaitement correspondu aux calculs effectué à l’aide des
formules d’
, après
avoir vérifié l’adéquation entre les deux calculs, il a effectué une vérification supplémentaire en
calculant directement les 20 digits hexadécimaux à la position 1 000 000 000 001 à l’aide de
l’approche par formules BBP présentée précédemment. Le résultat B4466E8D21 5388C4E014,
qui a requis 21 heures de travail, a parfaitement correspondu aux calculs effectué à l’aide des
formules d’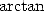 . Les digits hexadécimaux ont alors été convertis en base dix, une opération peu
triviale d’ailleurs, reconvertis en hexadecimal pour vérification, puis le record a été officialisé
[2].
. Les digits hexadécimaux ont alors été convertis en base dix, une opération peu
triviale d’ailleurs, reconvertis en hexadecimal pour vérification, puis le record a été officialisé
[2].
Les calculs (tout compris) ont duré près de 600 heures sur un HITACHI SR8000/MP doté de 1TB de stockage (1024Go), soit la même mémoire que pour son précédent record de 1999, alors que 6 fois plus de décimales ont été calculées !
5.2 Perspectives et motivations
Comment expliquer que la course aux décimales reste d’actualité ? Les motivations pour battre le record de
décimales de 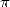 n’ont en fait jamais manquées, confinant même parfois à un soupçon de mauvaise foi. On
citera pêle-mêle le test des ordinateurs (un bug aurait été découvert par Bailey lors de son record de calcul
en 1986 sur des Cray-2), l’hypothétique apparition d’irrégularités dans la répartition des décimales
calculées (chou blanc de ce côté pour l’instant) ou la mise au point de techniques toujours plus
efficaces d’implémentation de calcul des décimales (la compétition fait actuellement rage sur
l’internet entre plusieurs mathématiciens informaticiens pour le titre de programme le plus rapide du
monde).
n’ont en fait jamais manquées, confinant même parfois à un soupçon de mauvaise foi. On
citera pêle-mêle le test des ordinateurs (un bug aurait été découvert par Bailey lors de son record de calcul
en 1986 sur des Cray-2), l’hypothétique apparition d’irrégularités dans la répartition des décimales
calculées (chou blanc de ce côté pour l’instant) ou la mise au point de techniques toujours plus
efficaces d’implémentation de calcul des décimales (la compétition fait actuellement rage sur
l’internet entre plusieurs mathématiciens informaticiens pour le titre de programme le plus rapide du
monde).
Chacune de ces raisons prise séparément n’est pas suffisante. Il serait probablement plus honnête de dire
que c’est la conjonction de toutes ces raisons, sans compter la passion engendrée par la “personnalité” de 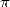 ,
qui alimente et renouvelle la compétition. Il est vrai que l’implémentation moderne des librairies
d’arithmétiques sur grands nombres (basées sur les techniques de FFT , de Newton vues précédemment)
doit beaucoup à la course aux décimales de
,
qui alimente et renouvelle la compétition. Il est vrai que l’implémentation moderne des librairies
d’arithmétiques sur grands nombres (basées sur les techniques de FFT , de Newton vues précédemment)
doit beaucoup à la course aux décimales de 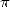 . Il est vrai également que la mise au point de
programmes efficaces n’est pas à la portée de n’importe qui et qu’il faut soigneusement connaitre
l’architecture de son calculateur pour espérer obtenir une performance intéressante. C’est un
challenge pour de nombreux informaticiens doués en maths (ou l’inverse !). Nous avons vu aussi que
la découverte récente de la formule BBP 18 avait ouvert un champ d’investigations théoriques
immenses.
. Il est vrai également que la mise au point de
programmes efficaces n’est pas à la portée de n’importe qui et qu’il faut soigneusement connaitre
l’architecture de son calculateur pour espérer obtenir une performance intéressante. C’est un
challenge pour de nombreux informaticiens doués en maths (ou l’inverse !). Nous avons vu aussi que
la découverte récente de la formule BBP 18 avait ouvert un champ d’investigations théoriques
immenses.
J’ajouterai que la popularité de 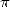 joue un rôle primordial : il est ainsi une justification peut-être
rarement avancée mais qui prend tout son sens auprès des simples amateurs de mathématiques membres de la
secte des adorateurs de
joue un rôle primordial : il est ainsi une justification peut-être
rarement avancée mais qui prend tout son sens auprès des simples amateurs de mathématiques membres de la
secte des adorateurs de 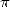 , ou même visible en écumant les forums de mathématiques de par le
monde : la théorie des nombres, l’analyse classique et les constantes ont une base accessible, au
moins en apparence, pour les non-mathématiciens et restent les plus grands fournisseurs de petits
exercices et de propriétés amusantes des nombres. C’est par ce biais que naissent beaucoup de
vocations de mathématiciens, et il suffit de consulter les pages web de mathématiciens comme
Bailey, Plouffe , Kanada ou des frères Borwein pour se convaincre qu’ils gardent à cinquante ans
passés une passion rafraichissante pour les constantes, parties visibles de l’iceberg mathématique.
La difficulté d’abstraction de certains autres domaines des mathématiques comme la géométrie
algébrique les confine probablement à un public davantage connaisseur et ils ne bénéficient donc pas
d’autant de symboles presque universels comme
, ou même visible en écumant les forums de mathématiques de par le
monde : la théorie des nombres, l’analyse classique et les constantes ont une base accessible, au
moins en apparence, pour les non-mathématiciens et restent les plus grands fournisseurs de petits
exercices et de propriétés amusantes des nombres. C’est par ce biais que naissent beaucoup de
vocations de mathématiciens, et il suffit de consulter les pages web de mathématiciens comme
Bailey, Plouffe , Kanada ou des frères Borwein pour se convaincre qu’ils gardent à cinquante ans
passés une passion rafraichissante pour les constantes, parties visibles de l’iceberg mathématique.
La difficulté d’abstraction de certains autres domaines des mathématiques comme la géométrie
algébrique les confine probablement à un public davantage connaisseur et ils ne bénéficient donc pas
d’autant de symboles presque universels comme 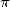 ou les nombres premiers peuvent l’être en
théorie des nombres. On rapprochera ainsi la quête des décimales de
ou les nombres premiers peuvent l’être en
théorie des nombres. On rapprochera ainsi la quête des décimales de 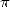 de celle du plus grand
nombre de Mersenne premier par exemple, exercice très à la mode actuellement (au jour où j’écris
ce texte, le record vient encore de tomber avec le 43ème nombre de Mersenne premier connu
!).
de celle du plus grand
nombre de Mersenne premier par exemple, exercice très à la mode actuellement (au jour où j’écris
ce texte, le record vient encore de tomber avec le 43ème nombre de Mersenne premier connu
!).
Mais il faut probablement laisser le mot de la fin à Genuys à qui on demandait, après son
record à 10000 décimales en 1958, pourquoi il avait choisi 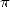 et qui répondit tout simplement
: “C’était pour moi un exercice de programmation, j’aurais pu choisir un autre nombre mais
et qui répondit tout simplement
: “C’était pour moi un exercice de programmation, j’aurais pu choisir un autre nombre mais
 c’était trop facile et
c’était trop facile et  (la constante d’Euler) trop difficile ! Et puis il y avait le record !”
[21].
(la constante d’Euler) trop difficile ! Et puis il y avait le record !”
[21].
 |
| François Genuys en 2004 |
References
[1] J. Arndt, C. Haenel, ”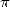 Unleashed”, Springer-Verlag, Berlin Heidelberg New York, 2001.
Unleashed”, Springer-Verlag, Berlin Heidelberg New York, 2001.
[2] D. H. Bailey, “Some Background on Kanada’s Recent Pi Calculation”, may 2003, preprint, http://www.nersc.gov/~dhbailey/dhbpapers/dhb-kanada.pdf.
[3] D.H. Bailey, P.B. Borwein, S. Plouffe, “On the Rapid Computation of Various Polylogarithmic Constants”, Mathematics of Computation, 1997, vol. 66, pp. 903-913.
[4] D. H. Bailey, R. E. Crandall, "On the Random Character of Fundamental Constant Expansions", Experimental Mathematics, 2001, vol. 10, no. 2, pp. 175-190.
[5] F. Bellard, “Computation of the n’th digit of pi in any base in 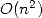 , unpublished, 1997,
http://fabrice.bellard.free.fr/pi/pi_n2.ps.
, unpublished, 1997,
http://fabrice.bellard.free.fr/pi/pi_n2.ps.
[6] L. Berggren, J. Borwein, P. Borwein, ”Pi : A Source Book”, Springer-Verlag, 2nd ed., 1997.
[7] J. Borwein, P. Borwein, “PI and the AGM: A Study in Analytic Number Theory and Computational Complexity”, Wiley, 1987.
[8] R. Brent, “Fast multiple-precision evaluation of elementary fonctions”, Journal of the Association of Computing Machinery, 1976, pp.242-251.
[9] D. J. Broadhurst, “Polylogarithmic ladders, hypergeometric series and the ten millionth digits of z(3) and z(5)”, 1998, preprint.
[10] S. A. Cook, S. O. Aanderaa, “On the minimum computation of functions”, Trans. AMS, 1969, vol. 142, pp291-314.
[11] J. W. Cooley, J. W. Tukey, “An algorithm for the machine calculation of complex Fourier series”, Math. Comp. 1965, vol 19, pp. 297-301.
[12] J.-P. Delahaye, ”Le Fascinant Nombre  ”, Bibliothèque Pour La Science, Belin, 1997.
”, Bibliothèque Pour La Science, Belin, 1997.
[13] P. Eymard, J.-P. Lafon, ”Autour du Nombre  ”, Hermann, Paris, 1999.
”, Hermann, Paris, 1999.
[14] X. Gourdon, “Computation of the n-th decimal digit of 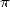 with low memory”, preprint, 2003,
http://numbers.computation.free.fr/Constants/Algorithms/nthdecimaldigit.pdf.
with low memory”, preprint, 2003,
http://numbers.computation.free.fr/Constants/Algorithms/nthdecimaldigit.pdf.
[15] X. Gourdon, P. Sebah, “N-th digit computation”, preprint, 2003, http://numbers.computation.free.fr/Constants/Algorithms/nthdigit.pdf.
[16] M. D. Householder, “The Numerical Treatment of a Single Nonlinear Equation”, 1970, MacGraw-Hill, New-York.
[17] G. Huvent, “Formules BBP”, 2001, Preprint.http://ano.univ-lille1.fr/seminaries/expo_huvent01.pdf.
[18] D. E. Knuth, “The Art of Computer Programming. Vol. 2: Seminumerical Algorithms”, Addison-Wesley, Reading, MA, 1981.
[19] L. Kuipers and H.Niederreiter, “Uniform distribution of sequences”, Wiley-Interscience, New York, 1974.
[20] J. C. Lagarias, “On the normalityof fundamental constants", Experiment. Math., 2001, vol. 10, no 2.
[21] “Le nombre 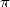 ”, Le Petit Archimède, Association pour le Dévelopement de la Culture
Scientifique, Amiens, 1980.
”, Le Petit Archimède, Association pour le Dévelopement de la Culture
Scientifique, Amiens, 1980.
[22] S. Plouffe, “On the computation of the 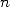 -th decimal digit of various transcendental numbers”,
unpublished, 11/1996.
-th decimal digit of various transcendental numbers”,
unpublished, 11/1996.
[23] E. Salamin, “Computation of 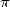 using arithmetic-geometric mean”, Mathematics of
computation, 1976, vol. 30, pp. 565-570.
using arithmetic-geometric mean”, Mathematics of
computation, 1976, vol. 30, pp. 565-570.
[24] A. Schönhage, V. Strassen, “Schennelle Multiplikation grosser Zahlen”, Computing, 1971, vol. 7, pp. 281-292.
[25] J. Tropfke, “Geschichte der Elementarmathematik”, Vierter Band, Ebene Geometrie, Dritte Auflage, Walter De Gruyter & Co, 1940.
Retour à la page d'accueil