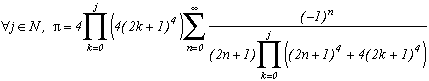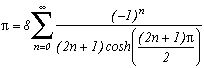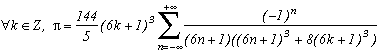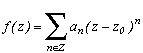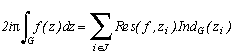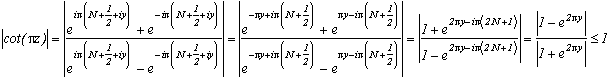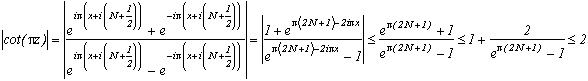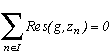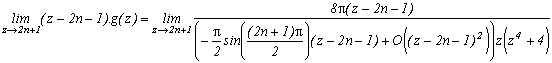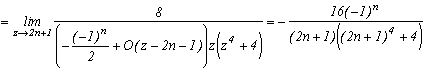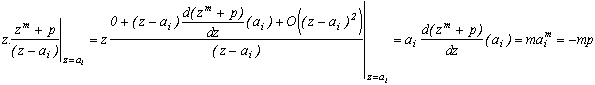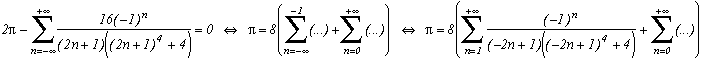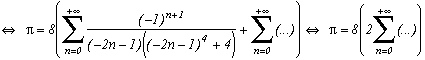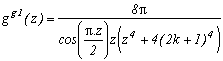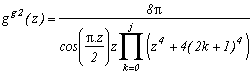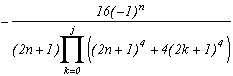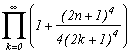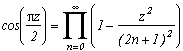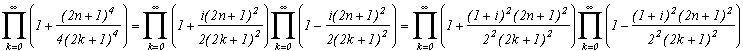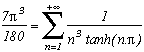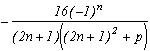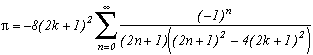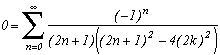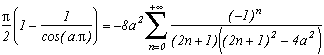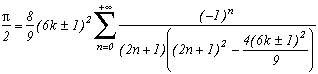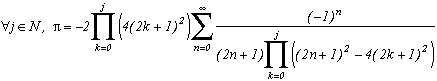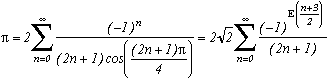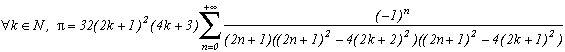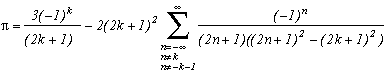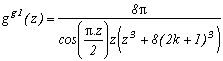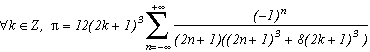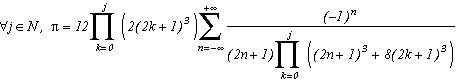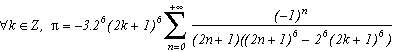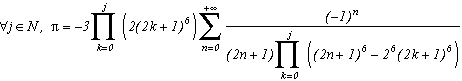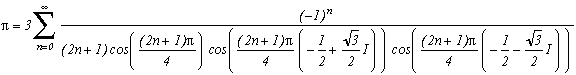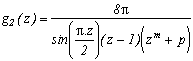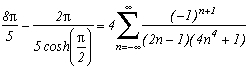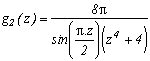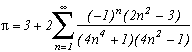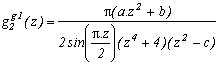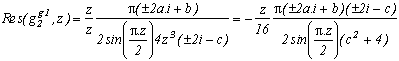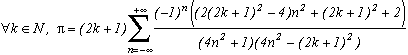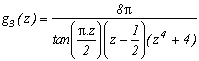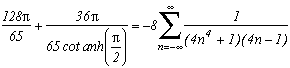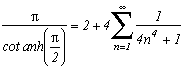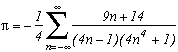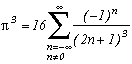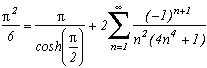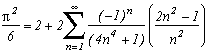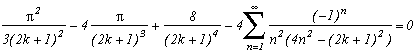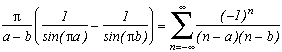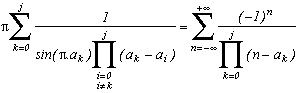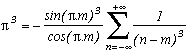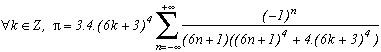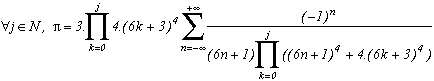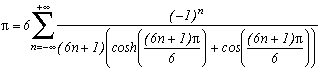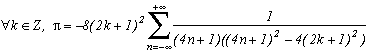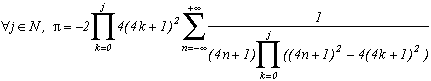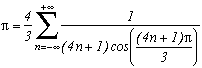Christian Frétigny

Some applications of the Remainders theorem
E. Estenave / C. Fretigny

I can not put them all down, there's too many of them ! You will discover them as you read this page. Nevertheless here are a few examples:

but also :



...

Around

The first serie at the top of this page for k=0 seems to be due to E. Estenave, Docteur ès Sciences, and was published by its author with two quite confusing proofs in a little book "Sur une série servant à définir approximativement le nombre Pi" ("On a serie allowing to define approximatly the number Pi") in 1901. Christian Frétigny, researcher and lecture at ESPCI in the field of quantum physics, found this book in a bookshop in Paris. He also told me that an exigeant and anonymous hand barred in pencil the word "define" and replaced it with "determine" with the annotation: "Speak french" ! (This makes more sense in French)
Anyway it stands that C. Frétigny offered this serie and one of its generalisation so to complete my collection, by showing me an other proof which used the remainders theorem. After reading upon the subject (I've never studied the holomorphes function, unfindable at uni!), we started a little correspondance in october as more and more series appeared using the same method. This page tries to synthestise the result of this exploration, of course very incomplete, seing the richness of the method. Several trails are offered, with at least one example for each of them, when the time or intuition failed to explore more deeply this idea.
We don't know if this is a complete study or a classification exist on this subject, or even if certain of those series, they have a poor performance, appear simply through rearrangement, or even if they are known (well, here we should get back to reality and Maple knows a fair few of them!) The calculating interes is not great, obviously, and this is why maybe I have not found those formulae, but the theory, the generalisation and the esthics of those series are very interesting. Without counting that we can reprove a good part of Euler's formulae very quickly.
To my knowledge, and with a bit of research, nothing exist on the web, so if you have some info, don't hesitate!

The Remaiders' theorem

First of all, lets us remember some definations before the famous remainders' theorem which is used for almost all calculation starting point:

The holormophes functions are complex variable functions on an open E of C in C, and differentiables. Let us place ourself in the more general case of meromophes functions, ratio of two holomorphes functions f(z)=g(z)/h(z), where the main problem is that h can be cancelled in certain z_i of course. So let those famous z_i with iI be the "poles" of f (that is to said rigourously that for all i of I, there exists a minimal integer n_i , called the pole order, such that (z-z_i)ⁿⁱf(z) is differentialble in z_i).
The general developpement of Laurent of a complex function, on a ring (space in between two circles, for convergence problem of the sum in + and -), is given by :

For the meromorphes functions, the summation is simply finite on the negative numbers, basicly the a_i are zero for i<(-N), N>0, N being the pole order of z₀.
We define the remainder of f in z_i as the coefficient a_-1 in the developpement of Laurent of f with z_i in the place of z₀. When z_i is a simple pole, this comes down to calculating :

For a pole of order m, we have the heavier formula :

Good, up till here, it's just been definitions, but what can we do with our meromorphe function that is getting bored?
Well we then consider a closed curve G of classe C¹ contained in E and which includes the poles z_i, iJ, JI.
We defined the indice of G in z_i (winding number) by :

which correspond in practical terms to the number of passage of the curve G (counted in the trigonometric sense) around the point z_i hence it's easy to calculate for nice contours.
Hence, finaly, the remainders' theorem gives us :

Intuitevely, this tells us that we can know the integral of f on a closed curve if we know the behaviour of f at it's singular points that are his poles. This surprising theorem is very important in complex analysis, and, as you are going to see, equally in the researche of series tending to !

Application of the theorem to a class of functions

In all the sequences, the curves used are simple squared curves, hence the indices of those curves at any point inside will always be 1 after the definition (useful !). Intuitevely, we have now on one side the sum of remainders, which will give us the series, and the other an integral, that we hope can be easily calculated. For certain functions, this integrals is null when we make the curve tends to infinity, it's this kind of functions we introduce as a class here :

Let . We consider a closed curve G(N), on which we are going to integrate, the square of the sumits : . We then avoid goingthrough the poles of cotan (denoted cot), that is the zeroes of tan(z), even more specific the nZ (phew..).

Let us now show that integral of g on the curve G(N) tends towards 0 when N tends towards infinity.
On the right hand vertical arm, z=N+1/2+i.y, y varying from -N-1/2 to N+1/2, we have :


because
and on the top horizontal arm, z=x+i(N+1/2), x varying from -N-1/2 to N+1/2, we have :

because exp((2N+1))-1>2 for N0 and
hence, on the two arms, cot(z)2, and since cot is odd, we can deduce we have this result on the whole curve. Since we are in R, we can put an upper limit on the integral with the length of the curve * the maximum of the function.
The square having for perimeter 4*(2N+1), we obtain :

But, for z on the square, for example of the right vertical arm, we have z=(N+1/2)+iy and
z(N+1/2) (similarly for all the other arms). We can even more affine :

Let us now tend the curve towards infinity, that is let us tend N to infinity or even z towards infinity for z on the squared curve. It remains to choose a function f such that and the integral will tend towards 0. This form reminds us a bit of Riemann's criteria for real series, and even, all functions f of the form of a rational fraction having a denominator degree greater than the numerator degree will do. In particular, all f of the form (z^a+c)^-1 with a>1 will do.

We used tan in g(z) but we can also look on the side of sin and cos. For cos, no problem if we put 1/cos in it's exponential form, since we have an upper limit exponential sum on the denominator in the same way as for cot.
To put an upper limit on 1/sin, we just need to use the relation , since we've put an upper bound on cot(z) in modulo by 2. We can still use the equivalent hyperbolic functions (cotanh, 1/sinh, 1/cosh) but this seems to be all.


We are now left with an integral tending to 0 if the curve tends to infinity. But this also means that all those poles z_n of our function g for n in I will be contained in this infinite curve.
The great advantage is that cot(z), as it's equivalents in 1/cos and 1/sin, admits an infinite number of poles, which here are the z_n=n for n in Z, and the sum of remainders at those point will hence produce an infinte serie.
After taking care of the integral which is null, and as we have since that the infinite indices of the curve at the poles z_i will be equal to 1, our dear remainder theorem comes down to choose f correctly :

Our objectives, since the series are going to have a slow convergence, is that at least they will be rational. Let us now examine a first application so to observe a simple method before explaining in more details why this works and then orientate the leads of research:

Preliminary example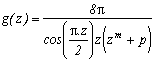

*** Case m=4 and p=4

It's really the one that works the most, hence I will detail the calculations, that I will definitely ignore afterwards! It is first of all clear that this function is contained in the previous studied case, it's integral on it's infinite curve is hence nul.
Let us now look at the poles of g and their remainders :
* 0 is a pole (for z in the denominatori), it's remainder is obtained by calculating
* The (2n+1) for nZ are the poles corresponding to the squares of cos, their respective remainders are :




Excellent, on one side, we have in the first remainder, and the other the sum of remainders in 2n+1 give a serie for nZ that is quite nice !

Yes, but the problem, there is still some remainders in g at the m-th roots of -p which are also the poles of g because they cancel z^m+p. It would be better if their sum was nice, most of them zero, will be perfect. In the present case the 4-th roots of 4 are 1+i,1-i, -1+i, -1-i, are simple luckuly, and that's what will limit the posibilities for other values of m.

* Let us calculate the remainders in those roots. Notice first, that in the general case, that when we manipulate a m-th root of p, do not forget that z^m=-p. But, with z(z^m+p) in the denominator of g, in the calculation of the remainder of g a m-th root of p, denote it a_i, we need to take the value in a_i of

Hence this term does not depend on a_i and only the cos will depend on it, the remainder of g in an m-th root of p is :
in our case m=4, p=4

But this, is a really good new because the sum of those remainders is nul. In fact, each remainder of a root is cancelled with the root of it's conjugate

We just now need to apply the remainder's theorem by writting that the sum of the remainder of g is nul :



and finaly (phew !)

Generalisation of the case m=4

Consider the function
(g1 for first type of generalisation) with k in N (or in Z but here, (2k+1)⁴ take the same value since k is negative because of the power 4)

Here and for the rest, I will use a little table to represent the poles and the remainders, it is still more clear than if the results are drowned in the middle of the text. Furthermore, only the sum of the remainders are important for the calculations, not the remainder of a root, except in particular case, since we know it's die to the sin that the sum cancel down. I will hence often odmit the expression of the only remainder of a root, especially during the generalisation, the result is quite annoying !

Poles	Remainders
0
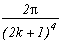
(2n+1)
+/-(2k+1)+/-i(2k+1)
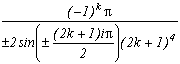
sum of the remainders of roots	0

Which allows us similarly to previous work to construct the following serie :

Note that if we make k tend to infinity, the ratio of the terms in front of the sum and the denominator tends toward 4, and we refind the sequence of Leibniz ! Ok, rigour is slightly overlooked since we did not justify the passage to the limit, but the note was valid especially for the intuitivity of the result.


Increasing the degree of the denominator

Harder !
The degree of the denominator, ignoring the z, is of 4 with the z⁴+4. Well, we can increase it so to make the sequence converge faster.
Let us consider the function :


Let us calculate the remainders :

Poles	Remainders
0
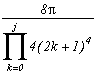
(2n+1)
sum of the roots' remainders	0

We then obtain the serie :



We can be interested in the limite case when j tends to infinity, this comes down to calculating the infinite product :
We can start for this from the well know expression (see for example the encyclopédie by Eric Weisstein) :

This is completly intuitive, since the infinte product is cancel as soon as z takes an odd value, hence it's a (2n+1) perodic function, this must be the cosinus... We have then :




and finally :

Of course, this is not really interested to calculate the decimals and here again rigour has been a bit forgotten, but the formula is quite esthetic, no?
Note that I think we can bring it back to the identities on the Riemann function foun by Simon Plouffe and the Borwein in 1997/1998 (see his personal page ). An identity used is in fact the sum

The proof is given on one of the pages if this site dedicated to Plouffe and other formulae of the same kind are there.

So, how does it works and how to continue ?

The major point to study is the one about the form of the m-th roots of p. We have seen that the cancellation of the sum of remainders for those roots depends on the transformation of cos into sin and that sin is an odd function. Since we start from a cos, we need a translation of since cos(x)=+/-sin(x).
In the previous example, since we start from cos(z/2), for the calculation of the remainder, the m-th roots of p needs to have a real part of the form (2k+1), hence integer and odd. This was the case previously for m=4 and p=4 since the roots were the +/-1+/-i.

This property essentially depends on the degree of the power of m through the form of the m-th untiy roots. To find the roots of z^m+p, we just need simply to multiply the m-th roots of unity by p^1/m.
If we denote a_k the real part of the k-th m-th root of unity, a sufficient condition for this to work is that there exist integer p such that

a_k.p^1/m=(2k+1)

and that this is valid for all the roots with the same p.
We will see later on that only m=2, m=3, m=4 and m=6 seems to work, because above degree 6, for example for degree 8 which seems favourable, we find one p for 4 roots and an other p for the 4 other roots, and nothing more work, we have a constant gap of 2^1/2 ! Note also that, to take advantage of integer solution,we will sometime inpractise be more interested in z^m+/-q^m.

And the generalisation - why does it work ?

When the degree m works and when we have found p, nothing stop us from multiplying p by (2k+1)^m, owe know we can multiply then the m-th roots of p by (2k+1), but since their real part is odd and that the product of two odd number is odd, the new roots have still the good property on their real part. This exaplain the generalisation on the previous example works.
It is not forbidden to put on the denominator as many polynomial of the form z^m+p(2k+1)^m as we want. This creates some product that increase the degree of the denominator and leads to some limiting cases as we have seen

So here was a brief overview of the principle of exploration, it is not impossible that some particular cases that do not fall in the abover hypotheses appears, but so far none has appeared. All the following example are hence varients on this principle. Here are the various leads that were considered :

Lead 1 : uses of cos, of z and an other polynomial of degree m : z^m+p, m>1 let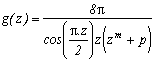

*** Case m=4 and p=4

This one, we have seen it as a preliminary example

*** Case m=2

* p=-4(2k+1)², p=-4(2k)², p=-4(6k+/-1)²/3

m=2 is a bit of a particular case, the simplicity of the roots allows us to study the general case while initially leaving p as a parameter in g. We will hence naturally find the values of p chosen above :

Here is the usual table :

Poles	Remainders
0
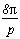
(2n+1)
sum of the roots remainders

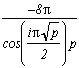
The i in the cos is very annoying if we want a nice relation and not land on some cosh with nastier effects. To cancel it down we just need to take negative p, and another i will come out of the roots.
Good, next we need to make sure we don't cancel down the cos on the denominator, we justneed a factor of 4 under the roots so to land on the cos that are multiples of which we know the value.
Finally, we can take a value p of either -4(2k+1)² or -4(2k)². And this choice is far from being random, see or yourself:

With p=-4(2k+1)² , we obtain for integer k , still by cancelling down the sum of remainders above :

But with p=-4(2k)² , surprise, we get :

because the remainder in 0 cancel downs the one with the roots since cos(2k)=1.
Hence wether we chose the odd 2k+1 or even 2k, we have a sum equal to or nul, this is an interesting phenomene !
In fact, more generally, if we choose p=-4a², we obtain according to the table of remainders the following very beautiful result, which explains our curiosity :

The only other rational value for the cos concern the value a=(6k+/-1)/3, which gives the new serie :

Increasing the degree of the denominator

this gives :


and for the limit case when making j tend towards infinity :

This last serie is already cited according to C. Frétigny in Gradshteyn, I.S. and Ryzhik, I.M. " Tables of Integrals, Series, and Products " San Diego, CA: Academic Press, 1996 (in CD version)
I unfortunatly don't have either the book nor the CD, but I think it will please me !

There is no limiting case for the second nul serie, we land on the sum of (-1)ⁿ whose result, if normally undeterminable, correspond intuitevely to the value 0 of the initial serie.

We can increase the degree of the denominator in more exotic ways. Since we have found a serie whoes sum is null. we can substract it from the serie giving Pi to find a new serie. Hence, we have :

* p=-(2k+1)²

There is this other interesting case for m=2. It correspond to the case where we know the denominator will cancel for the value n=k since we will get (2n+1)²-(2k+1)² in the serie. The order of the poles in z=+/-(2k+1) is then just 1. But we just need to calculate the remainders in those values with the differential formula given in the secion "Remainders' Theorem", and the remainders of the other values 2n+1 using classic methods, this gives :

Poles	Remainders
0
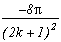
(2n+1) (n#k)
+/-(2k+1)

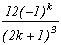
By cancelling the sum of those remainders, we can then write for all integer k :

The generalisation by increasing the degree of the denominator seems more complex simply because it force us to remove other values of n of the serie. We can see in all case that there exists no limiting case (because there would remain no values of n in the serie !!)

*** Case m=3 and p=2³

A very classical case, looks a lot like the case m=4, and easily generalised, it's in fact from here we are going to start since the case p=8 correspond to k=0 in the generalisation :
Remember the function used for this generalisation :



Here is the table of poles/remainder :

Poles	Remainders
0
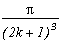
(2n+1)
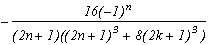
-2-4k (1st root)
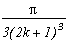
1+2k+/-I(2k+1)31/2 (the sum of the roots are cancelled)

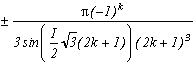
We can see, the only perticularity of this case is to have a first root independant of the others (due to the degree 3), but its remainder is perfectly usable, and we can form the sum (which was quite predictable !) :

A little varient anyway, the sum is this time down on Z, still due to the degree 3, the sum on N is not equal to the sum on Z^-. I think that it is for this reason that we don't need to just make k tend toward infinity to refind the sequence by Leibniz like before with the case m=2.
However, if we combine the sums on Z^- and Z⁺, we still manage to obtain a serie on N which is exactly the same as the one presented in the following section "Case m=6 and p=-2⁶"


Increassing the degree on the denominator

The principle is known now, let us avoid charging straight in this page is already long enough. We can with no problem apply the same process as for m=2 or m=4, we obtain for all integer j :

The limiting case does not seem easy to calculate due to the infinite product (is it even calculatable?), if someone has a result... All that we can say is that its a (2n+1) periodic function on R⁺ and not on R^-. This remind us a bit of the problem concerning the inverse of odd powers, that is the zêta function for the odd value.

*** Case m=6 and p=-2⁶

Last value that is apparently possible, this case does not give any theoritical difficulties. The roots of degree 6 are :
+/-(2+4k) which gives like in degree 3 a multiple of Pi
+/-(2+4k){j, j²} which has an odd real part, hence the cos is transformed as always into sin and the remainders of the conjugate roots cancel down.

We hence quickly move on, to fill in the table of poles/remainder and on the results :

Poles	Remainders
0
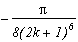
(2n+1)
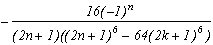
sum of the remainder of roots	0

This give :

Increasing the degree on the denominator

No problem here either, we easily get :

For the limiting case, we use the same procedure as for m=4, know that the infinite product of degree 2 is equal cos(z/2). The calculation is very hard and the size (already quite big) of this page significant, we are going to avoid to detail the calculations. To obtain the infinite product of degree 6, we are going to multiply three time this infinte product of degree 2 is worth cos, with z=(n+1/2), z=j.(n+1/2) et z=j²(n+1/2). We hence find :


The I will gives some developped cosh , (but it's not very nice, better leave this under it's compact form) which will assure a fast convegence.

Lead 2 : using sin, and an other polynomial of degree m : z^m+p, m>1 :

Since we have obtained odd series with the cos, that is with a (2n+1) in the denominator of the general term of the serie, we can expect to obtain some even series with the sin. But unfortunatly, not everything work out nicely...
En fact, contrary to the case (2n+1), 0 is a particular case of 2n, and the remainder in 0
is hence harder to calculate, it is in fact nul, does not appear anymore...
We need to find a trick, and shift the z on the denominator to z-1, that is consider the function
The 1 is chosen so to obtain a nice value of sin, but we could have an other shift, as long as its not in the form of 2n.
All of this is nice, but with habitude of this method, we can easily see that this shift will ruin our hope to find even series with this lead since we will have on the denominator something of the form q.n-a. Very bad...

*** Case m=4 and p=4

A big problem of this case, the shift stops the sum of remainders of the roots from completly cancelling down and we can see some cosh with harsher effects...
So let us see the pole/remainder table :

Pole	Remainder
1
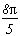
2n
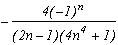
sum of the remainder of roots +/-1+/-i

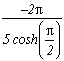
Which gives the serie :

We really need to get rid of this cosh term, otherwise the serie has not much use...
One solution is to write this term under the form of a serie as the same method of remainder, then bring back the two serie together.
Hence, we consider :

With the usual method, the remainder in 2n and the sum of those for the roots give the serie :

Side remarque, note the extraordinary purity of the serie on the right, of exceptional simplicity, and the horror of the left term! Does the form of the member on the left has a nice properties so to be equal to this kind of serie?

Still if we regroup the two previous equations, we get :

Yet another nice serie, but can we find another more satisfying result ?

Generalisation

How to generalise it ? As with the usual way with the (2k+1), we are going to try and be a bit more precise by introducing the function :

We are going to look for the condition on a, b, and c such that the sum of the remainders of roots of z⁴+4 cancell down.
For this, let us see the calculation of remainders for z=1+/-i (while not forgetting that z²=+/-2i and z⁴=-4)

Ok, we know that  z²=+/-2i hence, for the sum of those two remainders cancell down, we just need to use this property and that the terms after the z on the numerator is hence proportional to z, that is :

(+/-2a.i+b)(+/-2i-c)=4a-b.c+/-2i(a.c+b)=1+/-i

The serie previously considered correspond to a=1, b=-6 and c=1
The sum of the two other remainders cancel down because the square of the roots are real (+/-2).

Let us interest ourself now to the other poles, and sum using the remainder's theorem as always. For 2n, clasical calculation that I won't show.
Since the sum of the remainders for the roots of z²-c give , we have in all interest to choose c=(2k+1)² so that the sin be equal to 1, which gives after numerous simplification (phew !):

The original formula is the case k=0.

As long as it works, this method is not really made for the generalisation and depends mostly on the properties on the function. Here, the degree 4 is ideal for the roots 1+/-i have as a square +/-2i, which allows the cancellation of the remainder of the conjugated roots of z⁴+4.

The degree 2, 3 and 8 did not seem to be favourable, but there mst be a lot more to explore on this side !

Lead 3 : uses of tan and another polynomial of degree m : z^m+p, m>1

Intuitevely, the derivative of tan : (1+tan²) make us things that we can obtain some non-alternating series, unlike to the sin and to the cos. Because the (-1)ⁿ came from the expression of the derivative of cos and sin in (2n+1) or (2n). The use of the tan is very similar to the use of the sin, because their behavious are equivalent originally (noteworthy the poles are the same). Hence, we will come across the same problem as for the sin, and we can shift z to z-1/2 this time (for tan(/4)=1) so to avoid having a nul remainder in 0.

*** Case m=4 and p=4

Similarly as for the sin, it's the degree 4 which seems to work the most for the same reason. So let us bypass this quickly and run towards the results!
By considering :

we obtain the following pole/remainder table :

Pôles	Résidus
1/2
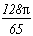
2n
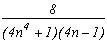
somme des résidus des racines +/-1+/-i

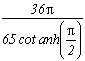
and the serie :

Then, studying the same function g₃ without the z-1/2 leads to a nice expression :

which, injected in the previous serie, gives :

I have not yet managed to generalised the result... and I have not yet tried with other degree than 4. If amateurs want to try !
Note that compare to the usual serie, we have this time 4n-1 instead of 2n+/-1. This research of other a*n+/-1 will be the object of lead 6.

Lead 4 : using z^q and an other polynomial of degree m : z^m+p, m>1 :

*** With no polynomial z^m+p

We consider first of all the functions with no polynomial of degree m, that is of type : or even with the cos or the tan.
Those functions are used to reprove the numerous formulae of Euler/Bernoulli. We will calculate the remainder in 0 with the differential formulae in the section "Remainders' theorem" for a pole of order m.
One thing to simply notice is that the sum on Z (without the 0 when we don't need it, of course) of the inverse of powers is null for certain powers due to the parity. Hence, this explain why for the sin and q=2, the remainder in 0 is not null and is equal to although it is for q=3. In fact, we have . And hence - now as we we are used to, we can even ignore the pole/remainder table - q=2 give :

More generally, for the sin, we can use the powers q=2k to give some series of the same kind as previously. The tan uses also q=2k and gives the non alternating series.
For the cos, it's obviously the same phenomene shifted since 0 is not the pole of the cos. We therefore need to use q=2k+1 so to find the sum of the inverse of odd powers. So, q=3 gives :

Which is really annoying, it's that the phenomene is the reason for which we can not calculate with this method the value of (3), Apéry's constant. And this is valid for all the odd powers, except for alternating series like the one above, unfortunatly, we can go from an alternative serie to a non alternative with the odd compared with the evens.

*** With polynomial z^m+p

Unfortunatly, things works a lot less here when q=1 (z only). The sum of remainders of the roots do not cancel down for example in the nice case of m=4 and p=4 even with the cos. We obtain a hyperbolic varient like cosh/sinh and we need again to use the trick like for the sin, that is to use the expression of cosh/sinh so to replace it in the serie.
But an other problem arrise : this expression, for example does not converge as fast as the one we obtain in the serie since we are varying the power of (2n+1)^q, expression missing in the serie with the cosh. And hence impossible to sort it our so to increasse the speed due to (2n+1)^q.
For example, by considering q=2, m=4 and p=4 and the sin :
we obtain the expression :

and the expression cosh above allows to obtain the serie :

But this is not really useful, and seems hard to generalise.


For certain powers q, we manage to cancel the sum of the remainders of the roots of z⁴+4 (for the cos and q=5 for example) but since however it does not want to work, the remainder in 0 is 1/192*(5⁴-96) and we can not isolate in this expression because the corresponding polynomial 1/192*x(5x⁴-96)=c does not have roots that can be express in radical form...

For the degree q=2, we have the same problem in the sense where we obtain a serie in the polynomial of second degree of the variable . But if we isolate , some square roots will appear but,  our original objectif was to stay in the rational series, hence with no roots. Having a serie of sum ² like as above does not give too much trouble, but if we start to introduce some roots, this page will have a length tending seriously towards infinity !
So I only give one example of what we can get :
q=2, m=2, p=(2k+1)² give :

Hence, we will stop there on this lead that seems to be a bit blocked if we stay on the original goal.

Lead 5 : using shifted poles for the polynomials

This method is very rich to obtain nice generalised formulae.It consist of taking a z we take systematically a z-a , of course understanding that we can then add other polynomial to the denominator. For the loading speed of this page (but will someone even get this far??), I will odmit some calculus details, when it is very classical.

Example 1 : two poles simply shifted
The study of gives :

And by making a tends to b, then b towards 0, we refind the serie by Euler (the very least we expect !)
The tan and cos (taken in z/2) gives exactly the same type of formula with the each of the charecteristic : tan instead of the sin and the non alternating serie for the tan, and cos instead of the sin and 2n+1 instead of n for the cos
The result is easily generalised for j+1 distinct on the denominator and this gives :

Unfortunatly, since the only rational values for the sin are taken for the rationals a_k in /3 and /2, in this study, we can not have more than two terms in the product and hence go further than j=1.

Example 2 : a shifted pole of order q

We will take q=3 here, because there does not seems to be any real general case that exist, the calculation depends on the used power. Hence consider the function . The application of the raminder method gives :

if I'm not wrong. The case m=1/3 or m=1/2 seems more interesting (and seems to be the only ones) if we want to obtain an expression with no irrational terms (not counting of course !).
We can also choose tan instead of the sin. We obtain :

Lead 6 : using a polynomial z^m+p, and seatch of coefficients a.n+/-1 in the denominiator of the serie

This lead was touch upon at the end of the third lead. Two methods can be used to achieve it :
* either we use a general shift (z+/-b) and then if we look on what values of b (of the form 1/r) allows to change the 2n+/-b into 2r.n+/1.
* or we shart from a shift inside the cos/sin that is c..z+d, such that the poles are directly in the form a.n+1.

The two cases are clearly equivalent because they both correspond to a shift, the second being more practical to find what will work and to form series.
Hence, if we look more at the second method, and if we base ourself still on the cancellation of the remainders of the poles of z^m+p, let us fix notation, and find a.n+1 on the denominator with cos(b.z+c.) that is the function .
Let us see the constrains :

1. Since we have z on the denominator, 0 is a pole and hence we need that the remainder in this pole, i.e. we want cos(c.) to be rational (no problems for the rationality of p !). This gives the condition (1) :

(1)

We exclud the case c=1/2 which gives one pole of cos (not practical !)

2. a.n+1 must be a pole, hence b..(a.n+1)+c.=(2n+1)/2 which is equivalent to condition (2) :

a.b=1 (2a)
b+c=1/2 (2b)

3. Finally, so that there is a transformation of cos in sin, the real part z₁ of z must satisfy the condition (3) valid for the generalisations :

(3)

Let us solve this system by using different possible value of c :
Note that c=0 is the case we have studied in the previous leads
this gives

c	c=0	c=1/3	c=-1/3	c=2/3	c=-2/3
b	b=1/2	b=1/6	b=5/6	b=-1/6	b=7/6
a	a=2	a=6	a=6/5	a=-6	a=6/7
z1	2k+1	6k+1	(6k+1)/5	1-6k	(6k+1)/7
Possible value of a.n+1	2n+1	6n+1	6n+5~6n-1	1-6n~6n-1	6n+7~6n+1

All is clear now ! Yet another remarque still, the form of z₁ forces us to consider only a degree 2, maybe 3. In fact, 4 roots can not have the same real part. We will see that there still exist a particular case for the degree 4.
But let us stay for the moment in the application of table, after clearing up, it's quite easy.

Hence consider the example of degree 3 with c=1/3 and b=1/6 (3rd columns of the table) :

gives the serie :

Unfortunatly, no increase of the denominator due to the degree 3, as we predicted in the 1st lead...

Otherwise there exist a particular case, the degree 4. The obligatory form of z₁ seen above stops the remainder of the conjugated 4th roots of z⁴+4 cancel two by two. But the sum of the four remainder is nul! I don't think this phenomene is found at any greater degree, this is due to the perfect symetries of roots for the degree 4, it's unfortunate...
Still by considering p=4*(6k+3)⁴, or even c=1/3 et b=1/6, we obtain the following serie :

And by increasing the degree on the denominator, we find :

And in the limiting case, we have :

The study of the sin is equivalent of the one of cos with a translation of /2, hence, we will not find any other new series there.
With the tan, the only possibility of non nul rational tang is for :
tan(/4)=1. By following the same reasoning as for the cos, we naturally find a serie in 4n+1, here for the degree 2, which seems the only possibility :

We can increase the degree on the denominator and obtain :

and the limiting case :

Other leads ?

With this method, we can see that we can reproof a fair number of formulae, and of course they are not all there !
We can look for other functions to put on the denominators some functions g. For example, we could put the complex exponential instead of the cos/sin etc... Only problem, exponential does not cancel down, so we need to couple it with a cos.
More generally, we can use functions which are not properly defined on the whole complex domain. For example, we can use cos(*log) so to obtain some series like the Simon Plouffe one because the logarithm is only defined in the complex domain if we cut part of it (supressing the right half from the origin) in the definition of the complex domain. Otherwise, we could turn around and have two different value for z and z*exp(2i) (log(z) and log(z)+2i). Which would be the least annoying !

A part from the polynomial, I have no other application ideas for the instant, but tell me if you do !