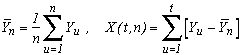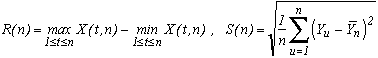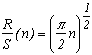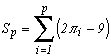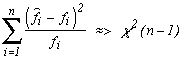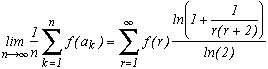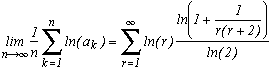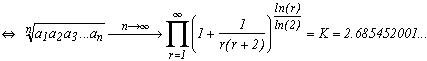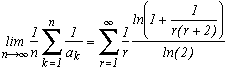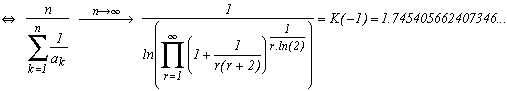|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|
Pi's decimals and Statistics
This last section of the triology of randomness is on the tireless research to, AT LAST, find something particular to Pi ! Because since we have been interested in our favourite constant, and invade its decimal that up till then have been protected, we need to admit that this sequence of digits, as if plucked from nowhere, is the most intriguing!
Ok, Pi is irrational, so we won't find the same periodic sequences...
But with a few not so complicated tools, we could maybe find other patterns??
Like the previous three, this page is meant to enrich itself with my collection, and of your eventual contributions!
Don't hesitate if you have a few more ideas or examples, tell me...
Here are the paragraphes tackled in order :
A - The fractal dimension1 - Estimation of the fractal dimension of a curve
2 - The rescale range methodB - Testing the decimals
C - Other approach
D - Bibliography
So, after a page on random theory, it is known that we know nothing at all on the decimals of Pi (in theory)!
Ok, but if we look directly at the decimals now, can we not find some strange structure somewhere, which are a bit out of the ordinary ?
Because, there must be something hidden behind the billions of decimal we have access to! As Gregory Chudnovsky said, it would be a disaster if the decimals would show nothing before the 1077 decimals that we are in thoery cabable to calculate if we used every atom in the universe ! And we are quite far, you can imagine, since we only found the 1011 decimals in september 2000 (206 billion).
The Chudnovsky wrote in 1991 that the decimals of Pi appeared to be more random than generated by a human, but still maybee not enough random!
The logarithm law iterate by Chung described on the page dedicated to randon phenomenon suggested to the same Chudnovsky to consider a random walk with the sequence of decimals (remember that with Donsker's theorem, the sum of a random walk converge roughly towards a Brownian motion). From there, we can construct fractals objects from the decimals of Pi, and why not measure their fractal dimendsions! Of course, that a great idea!
The fractal dimension of a classical procedure like the Brownian motion is 1.5.
Vanouplines, from Vrije Universiteit te Brussel (Belgium), demonstrated that the dimension of Pi is also very near 1.5.
The fractals are a very rich domain of mathematics, and my page on Mandelbrot shows that we can even find Pi in the Mandelbrot set!
The definition of a fractal, given by Mandelbrot himself in his booke "The fractal geometry of nature" (1983) is, as Weyl would say "a foggy fog"! :A fractal object is by definition an object whose Hausdorff-Besicovitch dimension is stricly greater than its topological dimension"
hum, thanks...
Mandelbrot states a bit later on that he still thinks that it would be better with no definition... :-)
On the subject of dimension, things are a bit more intuitive in euclidian spaces: a point has of course dimenion 0, a line has dimension 1, a plane has dimension 2, a volume has dimension 3, etc...
Only, all those dimensions are integers... Can you imagine some curves with rational dimension, or even real?
In fact, in a intuitive way the plane is full of an infinite number of lines. The line has no width, but if we make it curve in all direction, more and more tightly, the line will start occupying loads of space, and so it's fractal dimension is greater than 1, the limit hence being the plane of dimension 2. In short, the more the curve is crooked, and this no matter how much you zoom, more will the dimension of the curve be greater than 1.
A.1 - Estimation de la dimension fractale d'une courbe
Here we are using the "box count" method which makes use of the second definition of fractal objects by Mandelbrot, as vague as the previous one, but more intuitive :A fractal object is a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole.
Anyway, at whatever scale you choose, the object appears to be the same...
Take a coast on a sea map... this is a good example of a fractal curve!
So, if we take some squared paper of 1 millimetre, then a squared paper of 2 millimeters, and 4mm and finnaly 8mm. You understood it, the different sizes of the squares will be used to compare the drawing at different scales.... This is consistant with the form the different zoom used will produce which determines the complexity degree of a fractal object.
We take for each of those squared paper the same rectangular zone and we put on it the coast drawing. We then count the number of squares crossed by the curve and we take down the result in a table like the one that follows: (fictive data taken from [6])
Size of squares
Number of squares crossed
Size of squares*Number of squares crossed
(coast length)Decimal Logarithm of the squares' size
Logarithm of the coast length
Fractal dimension
1
6998
6998
0
3.845
1.39
2
2679
5358
0.301
3.729
1.35
4
1054
4216
0.602
3.625
1.32
8
424
3392
0.903
3.530
1.31
16
171
2736
1.204
3.437
1.33
32
68
2176
1.505
3.338
1.33
64
27
1728
1.806
3.238
1.44
128
10
1280
2.107
3.107
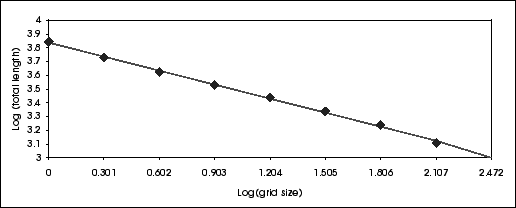
The coast length is longer when the precision is greater as we then find more twist on the coast. We can then see that the object can not be of high fractal dimension, but still it is neither 1.
By graphing the log of the coast length (5th column) against the log of the square size, we get a straight decreasing line whose gradient is 1 - D, where D is the fractal dimension. Intuitivly, this is expected. In fact if the gradient was 1, the coast length would be proportional to the precision wanted, hence there would have been no fractal criteria in the curve and D=0 in this case. Here, the gradient is negative as shown in the following figure, which means that the square size increase faster than the visible coast length decreases. In the above table, the dimension is evaluate for reach gradient between two points
With a gradient of -0.339 for the straight line, we get an average fractal dimension of D=1-(-0.339)=1.339.
So, now that we know what is a fractal dimension, the idea is to draw the random walk of the decimals of Pi and estimate it's fractal dimension.
Here is the graph where each decimals is linked to the previous and the next by a line :
Ok, but there still a major problem... It's that in the coast, the scale was the same in abscissa and ordered. Here, it's quite the opposite.... ouch!
But our friends the mathematicians thought about this problem and came up with the rescale range method in the 660s with Hurst, Mandelbrot and Wallis.
Hurst gave the following notations:
where Yi is the ie decimale of Pi-3.
He then define the two statistics :
And the best, is that our friend Hurst noticed that the statistic R/S often took a surprising form! In an emperical way, we get :
where c is a constant often taken to be equal to 1/2 and H is Hurst's exposant. This allows to keep the abscissa scale and to reduce the cummulated sum of the digits observed according to this scale.
But how to link it back to the fractal dimension ?
Well in fact, the relation between the fractal dimension D and Hurst's coefficient H isD=2-H
This is intuitevely understood since the higher H is, the more does the ration R/S ingrease rapidly with n. This means that the maximum amplitude increase more and more quickly compared with the variation, or more mundanely that the variation increase more slowly than the maximum amplitude. But this is nothing else but (for me!) the fact that we "zoomed" on the curve but that the variation did not follow, and so the fractal dimension decreases.
Still with our hands, an exposant H between 0.5 and 1 shows persistence sign in the curve, that is if it has experienced an increase over a certain period, this increase will probably carry on the next period. For an exposant less than 0.5 it's exactly the opposite with some agitations more chaotic and less predictable, this is logical since then the fractal dimension increase. It is therefore not surprising that for the procedure of finite independant variance, this exposant H if 1/2, (for example the Brownians mothion, which shows that their dimensial fractal is 1.5).
Anyway, and it's amazing to find Pi in this area, Feder showed in 1988 that for this procedur, we have exactly:
Incredible, no ??
For most of the natural phenomenon, H=0.72 hence D=1.28.
And for our good friend Pi ?
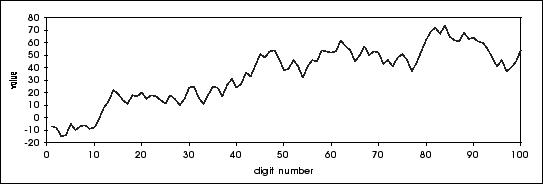
Instead of using the decimals of Pi, the average of the cumulated decimals is a more "continous" curve, which looks more like a random procedure. By denotingto be the ie decimale of Pi, we therefore consider the procedur :
being of course with digits between 0 and 9, the average expected is hence 4.5 and so 2
-9 should be close to zero on average.
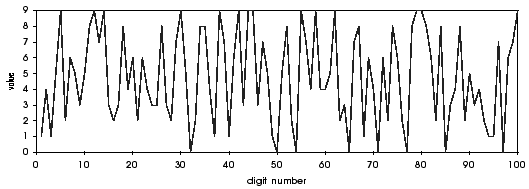
In fact, on the first 100 decimals, we get the following graph of Sp :
Well if this is not a beautiful procedur ?!
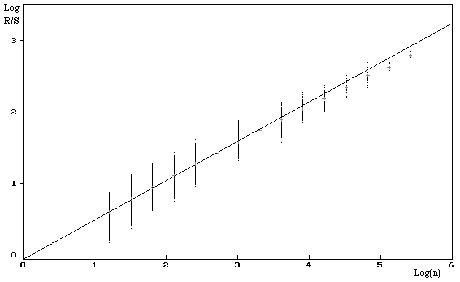
For 1.25 million decimals, we get the following curve with fractal dimension:
A clear tendance, which is provided by the curve the fractal dimension is 1.45. Yes, it's not a procedure with random increasement completely independant like the Brownian motion! There exists a little persistance (H=0.55), but to find out which one... hmmm...
So, the whole fractal dimension is a good indicator to tell us that obviously, something is going wrong! But it doesn't tell us what.... Let us examine a bit more the empirical spread of the decimals :
The fact that the decimals of Pi have no problem passing the most classic tests like Khi-squared, the poker test, and the arctan law does not help....
Euh.... by the way, what's all this ?
Ok, to tell the truth, the mathematicians have not found much - I don't blame them ! :-) - on the spread of decimals by studying the number Pi itself, through its appearance in the formulae or theories... The method, is then no more probabilistic but statistic, involves inversing the previous method and this time starting from the decimals to find singularity to Pi. And we have to admit that it's not that simple....
It's the most classical, and one of the weakest.... the statisticians tend to say that everything goes through a Khi-squared :-)
It's a statistic that works out the sum of the squared difference of the frequences observed with the frequence expected. Under the hypothesis that the data does follow the expected result, it follows as it names stated a Khi-squared with freedom degree of n-1 where n is the number of frequence we are considering :
fi is the expected frequence and
We don't have a freedom degree of n since the last frequence has to be known due to the others (the sum of the frequence is the number of decimals used, hence known!). Only n-1 frequences actually influence the statisctic calculation which is why we attribute a freedom of degree n-1 to the law. All of this can be proven of course, but it's not the idea of this page or even this site !
Then all is needed is to compare the value obtained with the value taken from the associated law. If this value is less than a fractal order of 0.95, this means that probability observed in nature of the value Khi-squared greater than this statistic is greater than 5%, etc... In short, this would imply that our constant has nothing exceptional....
And guess what happens!
Of course, nothing.... :-)
Here are the frequence observed for the first 200 billion decimales of Pi-3 :
Digit
Appearance in Pi Appearance in 1/Pi 0 20000030841
19999945794
1 19999914711
20000122770
2 20000136978
20000060451
3 20000069393
20000182235
4 19999921691
19999876817
5 19999917053
19999977273
6 19999881515
19999911742
7 19999967594
20000001035
8 20000291044
19999927489
9 19999869180
19999994394
Statisctics of Khi-squares 8.09
4.18
Those two statistics correspond to fractal order of 0.53 and 0.9 respectively. That is that we get respectively 53% and 90% observation in the statistic nature to take a greater value... Basically, nothing exceptional!
Note that those two statistics are calculated only on the first 200 billion decimals, so it's only to see if anything goes wrong! Because there could be a few variation and there are no reason for a decimal to appear more often than others, or less. So it's not very powerful !
Kanada, who calculate those 200 billions decimals, did the test by blocks of decimals, the files are available at ftp://pi.super-computing.org/. The Khi-squared test for the successive splitting of 10 blocks the 6 billions decimals available localy. But really nothing special...
So, let us continue our invistigation !
This statistic is a bit better than the Khi-square since it is interested not in each decimals, but in combination between decimals.
We put the decimals in blocks of 5, and in each of those blocks, we look to see what poker combination we find.
For this block, we either ger different decimals, or a pair, or three of a kind, a double pair, four of a kind, five of a kind (euh, quite hard in poker), or a full house...
This kind of test can be more funny than serious ! However, in nature we expect to find a certain number of paires, three of a kind, etc... This test is of higher level than the Khi-squared test in the regularity of the decimals combination frequence.
For 200 000 poker's hand for example, the expected frequences are the following :
Combinaisons Fréquences attendues Décimales différentes
ABCDE60480
Paires
AABCD100800
2 Paires
AABBC21600
Brelans
AAABC14400
Full House
AAABB1800
Carré
AAAAB900
Quinte
AAAAA20
Total 200000
To obtain those expected frequence, we just need to count the possible cases over the favourable case as we say in probability. Let us take an example with the 4 of a kind:
we have 1 in 10 chance of getting exactly A (10 decimales), an other 1 in 10 to get another A and so on, so by argument, we have a 1/104 chances to get AAAA. But it could be an A like it could be a C or an other digit, so we have 10 different possible cases, we multiply the total by 10, this gives 1/103. Then, we need to get an other digit that is not A, there are only 9 remaining, so we have a 9 in 10 chance to get it and so we multiply the total by 9/10. Finally we need to place this B with the A, since there are 5 places, we have a choice of 5 different possibility so we multiply the total by 5.
In the end we get:5*9/(10*103)=0.0045
Since we have 200 000 draws, the number of 4 of a kind expected is 200 000*0.0045=900, which is what was expected. Working methodically (so not like me), we should always get it, but it's true that it's not that easy and that a bit of practise is needed !
The principle is then to do a Khi-squared test on the result to compare them with the expected result. Kanada's team did those various test on the record of 6 billion decimals. We general group together the 4 of a kind and 5 of a kind due to the weak frequence of 5 of a kind, but this was not done in the following test. The Khi-squared considered hence has a freedom degree of 6, and we of course did it on 1 200 000 blocks of 5 decimals :
DECIMALE 1 2 3 4 5 6 7 8 9 10| TOTAL EXPECTED
----------------------------------------------------------------------------------------------------------------------------------------------
Déc diff 36294173 36290069 36290127 36286820 36290298 36289575 36294505 36289984 36281969 36282987| 362890507 362879996.98
Paires 60475840 60476864 60485069 60484354 60477375 60474120 60476577 60473797 60485057 60486104| 604795157 604799994.96
2 Paires 12956498 12958229 12954176 12962149 12961317 12963422 12962341 12963379 12959383 12960093| 129600987 129599998.92
3 same 8643856 8641687 8639415 8636938 8640244 8639352 8635473 8640375 8642190 8641230| 86400760 86399999.28
Full House 1078694 1080546 1079458 1079213 1079216 1080368 1078612 1080174 1078744 1078985| 10794010 10799999.91
4 same 539027 540460 539627 538583 539598 541309 540416 540236 540532 538638| 5398426 5399999.95
4 same 11912 12145 12128 11943 11952 11854 12076 12055 12125 11963| 120153 120000.00
----------------------------------------------------------------------------------------------------------------------------------------------
KHI2 7.98 3.27 5.10 6.36 1.46 6.67 6.74 2.03 5.30 5.99| 4.33
(FRACTAL 0.25 0.77 0.54 0.4 0.96 0.36 0.35 0.92 0.51 0.44| 0.64
APPROCHE)
So there was a decimal test, then a total test (that a good use of Khi-squared, we can test anything!). And we can see that there are nothing to be noticed, no fractal comming anywhere need 0.05...
At the most the gaps between the digit 5 is considered too weak ! :-)
Aie aie aie, this doens't simplify things, still nothing...
But let us push forward !
As the name states, this test cuts the decimals in blocks of 5 and calculate the sum of each block, This test is meant to show parts where for example there are more frequently high decimal would make higher sum more common than in nature, etc...
The expected results are follow up on the multinomial laws. But it seems simplier to find the result using good old logical reasoning...
You know that we estimate a probability by wanted cases on possible cases. This is a way to proceed
Let us start easily: take a block of 5 digits, so that their sum be 0, all 5 digits must be 0, so there are only one possibility! This is the number of wanted case. On the other hand, each of the 5 digits have 10 different possible value, so the number of possible case is 10*10*10*10*10=105. So the probability that the sum is 0 is 1/105. Since we have 1.2 billion blocks, this give1.2*109/105=12000
expected case, simple.
Ok, a second example not so trivial now because i know you've warmed up !
In the third case, we need the sum of the 5 digits to be 2. We get several cases :
Either two digits are 1 and we get C(5,2)=10 (2 choose 5, C(n,k)=n!/(k!(n-k)!) ) ways to choose them between the 5 digits. Using one of the multinomial laws M(5,0.1,0.1,...) we get 5!/(3!2!0!0!...)*1/(103102100100...)=10/105 the probability for this event, for advanced reader who want to speed up.
Or a digit is 2 and the four others are 0, this can be in 5 different ways depending where you put the 2. With the multinomial, 5!/(4!1!0!0!...)*1/(104101100100...)=5/105 is the probability of this event. In the end we have 15 different wanted case hence a probability for this event of 15/105 that we can get through two method, either by hand or by multinomial.
The expected number of "SUM=2" on 1.2 billion block is therefore1.2*109*15/105=180000
I tell you it gets funny very quickly to see if we have a little logic in counting or not, try it!
Still on the 6 billions decimals and breaking them in blocks of 600 millions decimals, Kanada's team got the following results :BLOC = 1 2 3 4 5 6 7 8 9 10| TOTAL ATTENDU
------------------------------------------------------------------------------------------------------------------------------------------------
SUM= 0 1216 1197 1193 1250 1200 1176 1196 1214 1152 1233| 12027 12000.000
SUM= 1 5923 6023 5957 5967 6017 6028 6077 6045 6047 5975| 60059 60000.000
SUM= 2 17848 18002 17896 17914 18100 17835 17874 18127 17887 17937| 179420 179999.998
SUM= 3 42128 41943 41885 42180 41659 41987 41697 42120 41935 42088| 419622 419999.997
SUM= 4 84093 83998 83899 83694 83827 84749 83906 84146 83647 82995| 838954 839999.993
SUM= 5 150933 151285 152040 150889 150914 151440 151465 151357 151106 150406| 1511835 1511999.987
SUM= 6 252052 251554 252425 252377 251639 251762 251674 252596 252215 252220| 2520514 2519999.979
SUM= 7 395189 396146 395922 396137 396044 395779 396032 396210 396185 395973| 3959617 3959999.967
SUM= 8 593637 592684 593729 594333 593971 593748 594449 594366 595328 593856| 5940101 5939999.951
SUM= 9 858470 858342 858321 856921 858350 859226 857611 857056 857478 858960| 8580735 8579999.929
SUM= 10 1194437 1195429 1194514 1194536 1193553 1194870 1194976 1194134 1193540 1194598| 11944587 11951999.900
SUM= 11 1605266 1607515 1608231 1607348 1608394 1605279 1609486 1608762 1609340 1609442| 16079063 16079999.866
SUM= 12 2091618 2095708 2094196 2092715 2093180 2091291 2095945 2093030 2093830 2092915| 20934428 20939999.826
SUM= 13 2648030 2646321 2645322 2643188 2647514 2646881 2644930 2645962 2643577 2643418| 26455143 26459999.780
SUM= 14 3252283 3252822 3249652 3253274 3250272 3253381 3249525 3252776 3253078 3250408| 32517471 32519999.729
SUM= 15 3899546 3898175 3893160 3893092 3898171 3894389 3895990 3897963 3895193 3892981| 38958660 38951999.675
SUM= 16 4551996 4551347 4554651 4553603 4553925 4552191 4556515 4553971 4552146 4553568| 45533913 45539999.621
SUM= 17 5201733 5201032 5201711 5203465 5201273 5206295 5205467 5202503 5205968 5204304| 52033751 52019999.566
SUM= 18 5809804 5806104 5812753 5808793 5810430 5805164 5806757 5809698 5808856 5811122| 58089481 58079999.516
SUM= 19 6335116 6335295 6334714 6340044 6337456 6338388 6334646 6335387 6333802 6337037| 63361885 63359999.472
SUM= 20 6753880 6755164 6757793 6756423 6757089 6754552 6754976 6757225 6758836 6754169| 67560107 67571999.437
SUM= 21 7048473 7047684 7054697 7049417 7047712 7050818 7055967 7052409 7047565 7049867| 70504609 70499999.413
SUM= 22 7195837 7204989 7194831 7199905 7198519 7203840 7196208 7201386 7198388 7201909| 71995812 71999999.400
SUM= 23 7203470 7201800 7195852 7197458 7200117 7198749 7199849 7195443 7198608 7197627| 71988973 71999999.400
SUM= 24 7050060 7047213 7049745 7048952 7051751 7051705 7051021 7045667 7046796 7052240| 70495150 70499999.413
SUM= 25 6761856 6760420 6761986 6763441 6754330 6755526 6758730 6761985 6763792 6756381| 67598447 67571999.437
SUM= 26 6335540 6335738 6337255 6332486 6337542 6333532 6337991 6336563 6336177 6338455| 63361279 63359999.472
SUM= 27 5808627 5808453 5807373 5807508 5808064 5810369 5804582 5805840 5805965 5810139| 58076920 58079999.516
SUM= 28 5202613 5202126 5204017 5200678 5197496 5202708 5204795 5201079 5205991 5202461| 52023964 52019999.566
SUM= 29 4555210 4553387 4553230 4555919 4557110 4552793 4553511 4554100 4554409 4553357| 45543026 45539999.621
SUM= 30 3895961 3892915 3894162 3894606 3894262 3894426 3892307 3894606 3894956 3895352| 38943553 38951999.675
SUM= 31 3256018 3250243 3251867 3249837 3253079 3249265 3253032 3249406 3252452 3253948| 32519147 32519999.729
SUM= 32 2644512 2648978 2647511 2648128 2643971 2644766 2643985 2645457 2645607 2644185| 26457100 26459999.780
SUM= 33 2093395 2095113 2096225 2095226 2092831 2094830 2093681 2095801 2093199 2095237| 20945538 20939999.826
SUM= 34 1607321 1609097 1608165 1609658 1608917 1608961 1606667 1607598 1608289 1608217| 16082890 16079999.866
SUM= 35 1195598 1193679 1193808 1195018 1196316 1196777 1195415 1195170 1195168 1193806| 11950755 11951999.900
SUM= 36 857619 858681 856824 858062 858473 859108 856967 857623 856698 857784| 8577839 8579999.929
SUM= 37 594438 594375 594600 593669 594880 595027 594359 594477 594675 593578| 5944078 5939999.951
SUM= 38 394990 395440 395415 397078 396760 396359 395443 396010 395884 395526| 3958905 3959999.967
SUM= 39 251920 251551 251452 252773 252682 252077 251600 252275 252268 251785| 2520383 2519999.979
SUM= 40 150416 151017 150658 150839 150496 150787 151427 151874 150468 151099| 1509081 1511999.987
SUM= 41 83539 84096 83381 84021 83994 84005 84573 83593 84225 84090| 839517 839999.993
SUM= 42 42301 41678 41976 42218 42204 41926 41479 41954 42097 42034| 419867 419999.997
SUM= 43 17972 18008 17838 17777 18371 17881 18101 17928 17898 18073| 179847 179999.998
SUM= 44 5958 6047 5932 5986 5964 6105 5937 5930 6026 6029| 59914 60000.000
SUM= 45 1158 1186 1236 1197 1181 1249 1179 1178 1253 1216| 12033 12000.000
Hum, still nothing interesting.... hopeless...
Kanada's team did one more test, called the Gap test but I never understood it! If someone can explain to me? The files which explain it is on this adresse.
The arctan law test also remains a mystery for me and I haven't found any reference to it on the web which discusse it. Well since we can't invent everything yourself (!), I take my leave, I will wait for a nice soul to come an help me....
Let me say that numerous are the graphical method used to try and find regularity in the decimals. For example change the decimals into binary and put them end on end in a square to see if they make a picture. If the landscape produced seems more regular thant if made by pure chance, the Chudnovsky have not found any satisfying explenation to this kind of phenomena...
Here is a quick tour of classical statistical method to analyse decimals
Quite a few crazy ideas have been passed in the domain of singularity research. A few ideas sometime are worth attention, like the one that consiste of using the knowledge of a number group in general to test if this group belong to a particular constant. A good example uses Khintchine's constant.
Aleksandr Khintchine publishes in 1935 a little bookled on continued fractions, ("Continued Fractions", why complicate the title ?) in which he notes that the geometric mean of the coefficient of of a continue fraction tends to a certain constant, and this is often certain (except for a set of number with measurment null, the measure being Lebesgue one)....
In English and in clear (because this site is not a theory lecture on measure!), this means that this result is true except for a set of isolated numbers, with no continuity between them, even of infinite size (like N or Q). There exists of course a few exotic sets that did not fit this intuitive explination but that's not the point.
In general, he showed the following theorem :
Khintchine's theorem
Suppose that f(r) is a funtion of positive integer r and suppose that there exists two positives constants C and d such that
In other words, f increases not as fast as the square root.
Then, for nearly all the number in the interval [0,1], by denoting ak the coefficients of their regular continue fraction, we have the following equality :
The proof of this theorem, which takes several pages of the book by Khintchine, seems a bit too ambitious for this site, but if one day I have the courage, I will put it up maybe!
There exists other version based for example on ergodic theory, which is not that surprising seing the shape of the result.
We observe that the conditions on f is sufficient to make sure of the convergencce of the element on the right whose term in the serie at infinity is equivalent to f(r)/r2.
We now take a function f which satisfy the hypothesis of the thoerem, the logarithm.
We then get that for nearly all the numbers in [0,1] :
And here appear the famous Khintchine's constant... It is a very interesting one by the way, but if we start going off topic, we'll never finish! Still see the reference of the bibliography to know a bit more.
Not easy to do calculation with this expression. But Bailey, Borwein and Crandall recently managed to get 7350 decimales of K with the help of the Zêta functions which converges a lot faster.
We can also obtain a formula with the harmonic mean and f(r)=r-1 :
We could also get a K(-2) by taking f(r)=r-2 etc....
This second formula for the harmonic mean is also a result "mostly true", so a small set of numbers ("negligible" for probability) donc satisfy this formula. Ok, all those fractions with coefficients very easily defined sequences will be part of this negligible set (think of the number e for example, or the golden ration, who trivially don't satisfy the two formulae of geometric or harmonic mean)... but what is the shape of the set of sequences such that the geometric mean don't tend toward the considered expression? It's a simple question of analysis, no?
And even if we know that numbers that don't follow this result are very rare, the idea is to check if the coefficient of the continu fraction of Pi do follow that result.
In all, another way to find a particular group to fit Pi into. Surronding it one way or the other!
David Bailey said to this that the coefficients of the continu fraction of Pi don't seems to follow a pattern and are supposed to be random in a certain way.
We now know 17 001 303 coefficients of the continu fraction of Pi of which the first are Pi = [3; 7; 15; 1; 292; 1; 1; 1; 2; 1; 3; ...]. The geometric mean of those coefficients is 2.686393 and the harmonic mean is 1.745882. The are approching the constant of K and K(-1) even if the calculation is done on only 17 millions coefficients, which is quite small compare to infinity !
So here again, no conclusion can be drawn...
We can see with Khintchine's constant, taking the senic route through fascinating theories on the general behavious of numbers, mathematiciens tried to observed if Pi behaved in a particular way. The tools of statistic study of decimals being very limited and not having given much, it's a new very interesting approach.
The decimal quest will most probably not bear any fruits to this study parodoxly because there is no reason why after 207 billions of decimales, sundunly we find a pattern that is so obvious!! It's still the dream of many mathematicians after all, so you never know....
But the pattern is probably already in front of our eyes which are wide open, but either still not enough, or there doesn't exist one and we will never know if we can prove a really strong result such the normality of the decimals of Pi. And even, Pi would not be Pi without ITS own decimals, and not one different! The normality is not all, it doesn't trivialize completly and definitly the number.
Similarly for the representation of Pi in continu fraction. But this idea of representation is interesting. We have seen with the decount algorithm that there exists some bases where Pi is one of the simplest number, that is remarquable! The more ways we find to represent the numbers and the nnumber class associated with those representation, the more of an idea we will have of Pi and it's place with the numbers will be more precise. So for me it's still a very open domaine...
4 references of reference !
[1] Laboratoire de Kanada, Archives de Pi - Super-computing.org
ftp://pi.super-computing.org/
[2] Patrick Vanouplines, Université libre de Bruxelles, Rescaled range analysis and the fractal dimension of Pi.
http://gopher.ulb.ac.be/~pvouplin/pi/pi.ps
[3] D. Bailey, J. Borwein , R. Crandall, On the Khintchine Constant
http://www.nas.nasa.gov/Research/Reports/Techreports/1997/PDF/nas-97-030.pdf
[4] "La constante de Khintchine", miroir basé à l'Inria du site de Steven Finch
http://pauillac.inria.fr/algo/bsolve/constant/khntchn/khntchn.html
back to home page