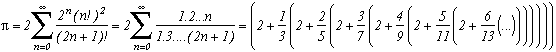Stanley Rabinowitz

The spigot algorithm
A. Sale - D. Saada - S. Rabinowitz

So, what is this algorithm?
Well, let's remember that we know pi in its decimal form, which is in base 10:

Pi=3.141592653589793238462643383279...
this can also be written as :

This is known as Horner's form; it allows us, among other things, to reduce the number of multiplications when evaluating a polynomial. We can see here that it is base 10, and that the base's step is constant, meaning that we have 10 at each decimal place (digit if base different from 10). We note this base [1/10,1/10,1/10...]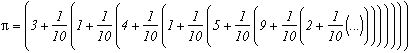
Now, let's consider the series discovered by Euler (See page about him for the demonstration) and let's write it in Horner's form:


Now this is interesting, if we compare it with the previous expression, we can see that we are considering a base with a changing step [1,1/3,2/5,3/7,4/9...]. And in this base, Pi is [2;2,2,2,2...]. So in this base, Pi is one of the simpliest numbers that exists !
We know Pi 's digits in this base, so to compute Pi 's decimal places in base 10 one by one, one just needs to build an algorithm that changes it to base 10, which is precisely the principle of the spigot algorithm.

A historical overview of this method

I might as well tell you that I haven't found much information about the above mathematicians! We can't always find what we want on the web, and if someone doesn't have a personal page, it limits what one can find out about him.
Initially, it was A. Sale who had the idea of this method in 1968 and used it to compute e.
Then D. Saada suggested applying it to Pi in 1988 and so did S. Rabinowitz in 1991. The latter is quite well known, he's a confirmed hacker, and even a mathematician who has published quite a few articles (He is a Mac friend by the way). He studied some of the finesses of this algorithm with his collegue Stan Wagon in 1995 in an article in the Mathematical American Monthly.

Around :

First of all, a little computation concerning how much memory it will take. In Horner's form, we can see that the n/(2n+1) step of the base is slightly under 1/2 every time. The exact value 1/2 would bring us to consider base 2. For the conversion from base 2 to base 10, we will need roughly Log₂(10ⁿ)=3,32n digits. We can consider it is about the same value for our base with a changing step to base 10. So if we want to get n décimal places, we will have to consider 3.32n boxes. To get 4 décimal places (including the 3 before the decimal point), we build a memory table of about 14 columns. In fact, 13 will be enough here. The translation of this algorithm would bring us to consider a table like this:

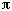
A		r	1	2	3	4	5	6	7	8	9	10	11	12
B	=		3	5	7	9	11	13	15	17	19	21	23	25
Initialization		2	2	2	2	2	2	2	2	2	2	2	2	2
*10		20	20	20	20	20	20	20	20	20	20	20	20	20
carried over		10	12	12	12	10	12	7	8	9	0	0	0	0
sum	3	30	32	32	32	30	32	27	28	29	20	20	20	20
remainder		0	2	2	4	3	10	1	13	12	1	20	20	20
*10		0	20	20	40	30	100	10	130	120	10	200	200	200
carried over		13	20	33	40	65	48	98	88	72	150	132	96	0
sum	1	13	40	53	80	95	148	108	218	192	160	332	296	200
remainder		3	1	3	3	5	5	4	8	5	8	17	20	0
*10		30	10	30	30	50	50	40	80	50	80	170	200	0
carried over		11	24	30	40	40	42	63	64	90	120	88	0	0
sum	4	41	34	60	70	90	92	103	144	140	200	258	200	0
remainder		1	1	0	0	0	4	12	9	4	10	6	16	0
*10		10	10	0	0	0	40	120	90	40	100	60	160	0
carried over		4	2	9	24	55	84	63	48	72	60	66	0	0
sum	1	14	12	9	24	55	124	183	138	112	160	126	160	0
remainder		4	0	4	3	1	3	1	3	10	8	0	22	0

And now let's explain how and why it works !
We recognise in the two first lines the numerator and the denominator of the steps of the changing step base. In the third line, we find Pi 's expression in that base. And we fill the last column of the remainder line with 0 's.
The algorithm to convert from right to left in the table is as follows :
Formally, the general principle consists in multiplying the digit by 10 and in computing the remainder in an equivalent of a Euclidian division of this number by the step of the changing step base. A number carried over will then appear at each calculation and comes from the same phenomenon which appears when one multiplies 53 by 8; firstly one multiplies 3 by 8, then one carries over 2 and adds it to the multiplication of 8 by 5 which is the multiplication of the next digit.

Filling in the red column for example :

1) First we fill in the *10 line by multiplying the previous line by 10. No problem so far !
2) We place in sum the sum of the *10 line with the carried over line, which is:

20+9=29 3) We do the Euclidian division of the sum by the number in line B of the same column :

29=17*1+12 4) We place the 12 remainder in the remainder line. Then we multiply the 1 quotient with line A and put the result in the next column's carried over line :

1*8=8 The 9 remainder of the red column comes from the previous column's computation. And so here we pass on the 8 remainder to the next sum's computation.

By repeating the process with the other columns, we fill in the first table and we get 30 as the last sum. But as we multiplied everything by 10, we take 3 as the first digit of Pi. That's it!

One little remark however : We can consider that a number in the last column is right if it is not followed by a 9.
When the remainder in the r column is higher than 100, we can obtain (but it is very rare...) 10 after the last decimal place that we take for Pi. We then take this digit plus 1 as digit for Pi, It's as simple as that!

Other formulas ?

Well I think any rational series should be all right as long as in it's Horner form, we only find integrers as expression of Pi in the changing step base (for the previous series, we only had 2's). Particularly, Ramanujan rational series should be able to be used and give a better algorithm.
Gosper's page's formula is also valid :


As the fraction of two terms of the series is always smaller than 1/13, we will need Log₁₃(10ⁿ)=0.9 boxes to get a digit. So if we consider 6 boxes, we can hope to get 6*1/0.9=6.6 decimal places, so 6 or even 7 decimal places at best. We can see that this is respected perfectly in the table because we even obtain 7 décimal places :

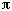
A		r	1	6	15	28	45
B	=		60	168	330	546	816
Initialization		3	8	13	18	23	28
*10		30	80	130	180	230	280
carried over		1	0	0	0	0	0
sum	3	31	80	130	180	230	280
remainder		1	20	130	180	230	280
*10		10	200	1300	1800	2300	2800
carried over		4	48	75	112	135	0
sum	1	14	248	1375	1912	2435	2800
remainder		4	8	31	262	251	352
*10		40	80	310	2620	2510	3520
carried over		41	12	120	112	180	0
sum	4	41	92	430	2732	2690	3520
remainder		1	32	94	92	506	256
*10		10	320	940	920	5060	2560
carried over		5	30	45	252	135	0
sum	1	15	350	985	1172	5195	2560
remainder		5	50	145	182	281	112
*10		50	500	1450	1820	2810	1120
carried over		9	54	75	140	45	0
sum	5	59	554	1525	1960	2855	1120
remainder		9	14	13	310	125	304
*10		90	140	130	3100	1250	3040
carried over		2	6	135	56	135	0
sum	9	92	146	265	3156	1385	3040
remainder		2	26	97	186	293	592
*10		20	260	970	1860	2930	5920
carried over		4	36	90	140	315	0
sum	2	24	296	1060	2000	3245	5920
remainder		4	56	52	20	515	208