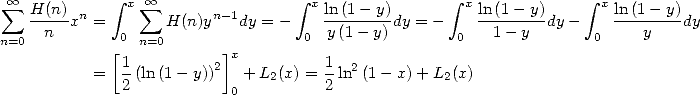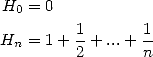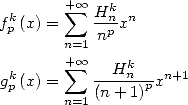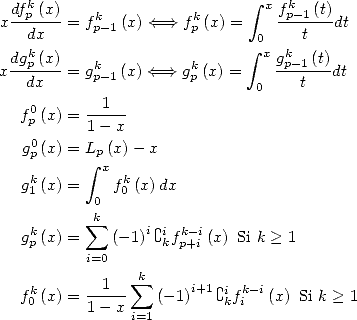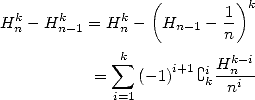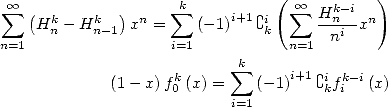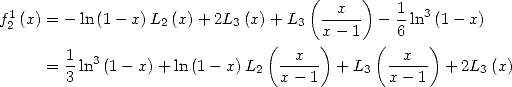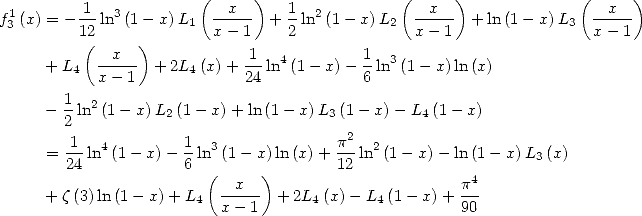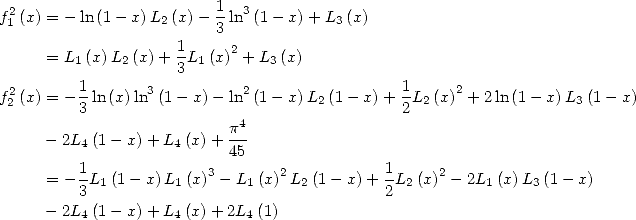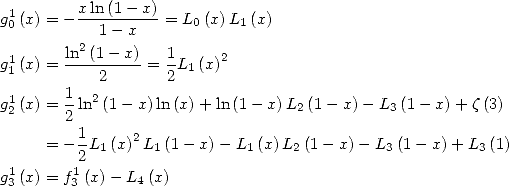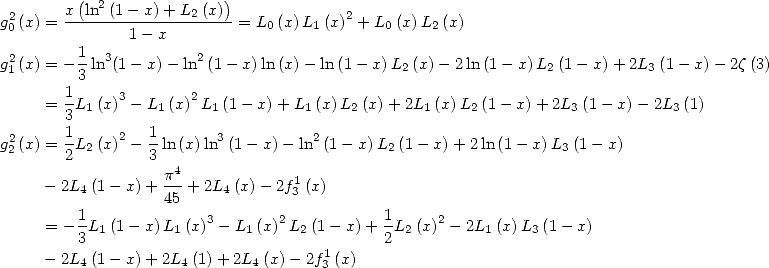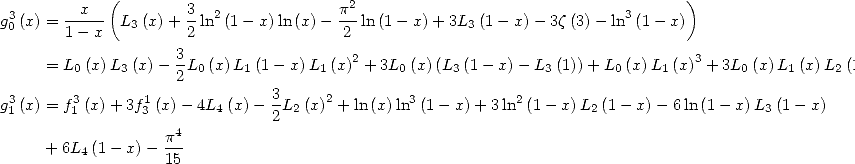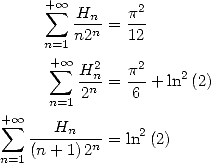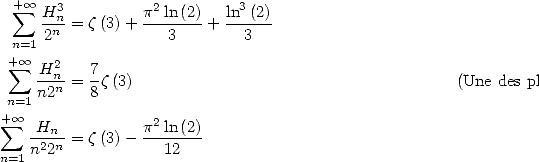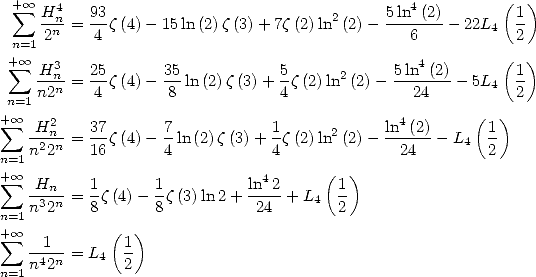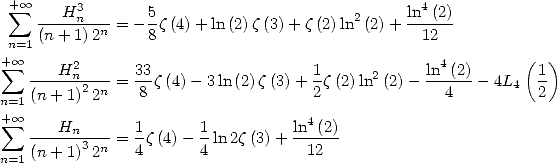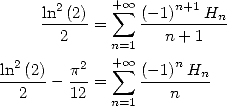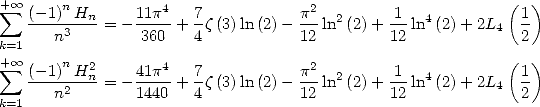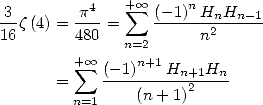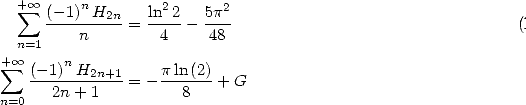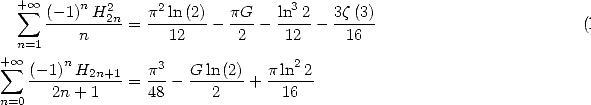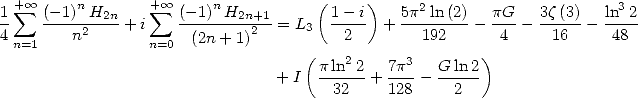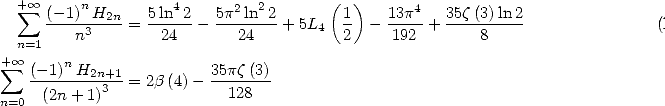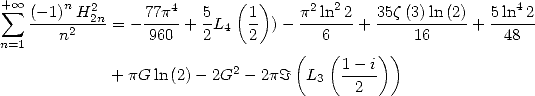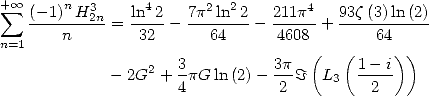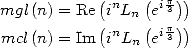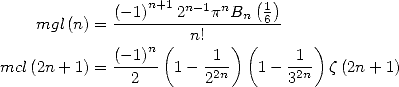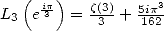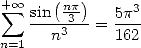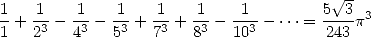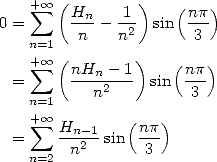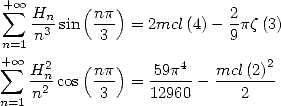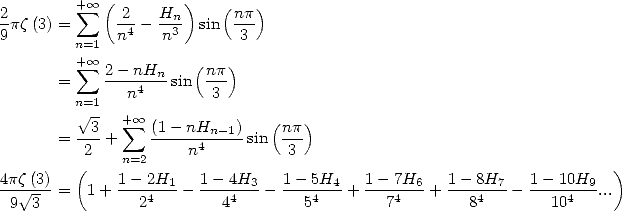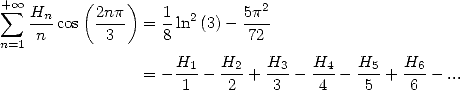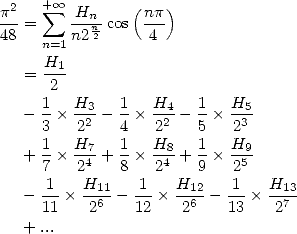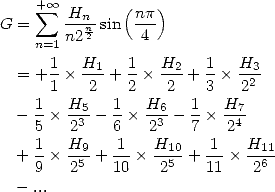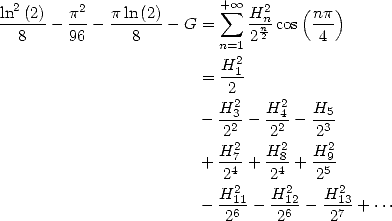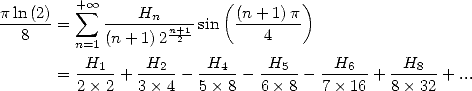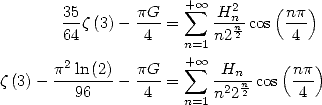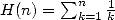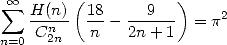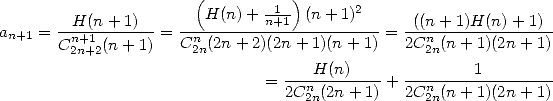13 Harmonic Series

The BBP formulae are expressed for example as linear combination of those hypergeometric functions but even more things await us! Because thanks to integral representation, we can also in fact obtain harmonic series of the same form as all those that we just found.

The harmonic series are those which the terms contain the harmonic sum .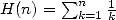

13.1 Links between harmonic series and the polylogarithms

We have seen that the BBP or factorial formulae are integral combinations of the kind .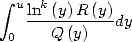

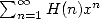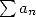Let us now consider the integral equivalent to the serie's term of the harmonic sum . According to the product formula by Cauchy for which two absolutly convergant series and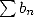

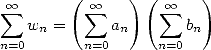(587)

where 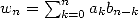, by choosing 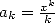and 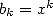we get 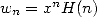and so

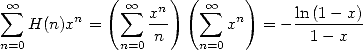(588)

You can start to see what I mean... :-) As soon as an integral uses this kind of formula, we will have some harmonic lurking in a corner. Here, we find one immediatly in 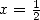the formula

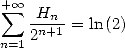(589)

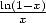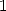With we had some polylogarithm (voir 35), but this doesn't matter, we divide the expression 588 by x ! And then integrating between and , we have

But, since 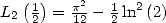, we finaly obtain that

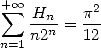(591)

Impressive, no? obviously, this remind us of many things, we are swimming in a sea of polylogarithm and logarithm...

We can study in more generality the harmonic series of this kind and the formulae that follows from them by introducing the notations by Gery Huvent (him again !). All the following formulae which are not yet known can be credited to him !

13.2 Study of 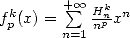and of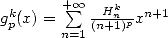

13.2.1 Definition, remarquable relations

We let

Those series have a convergence radius of 1. The convergence take place on the border as soon as 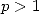(because 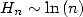). Then

Proof.

hence

Similarly

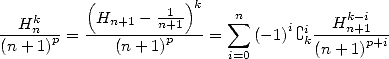(605)

 _

13.2.2 Calculations of certain functions

A usual expansion (donne by Cauchy's product) gives

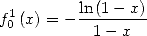(606)

Then by integrations

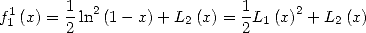(607)

and

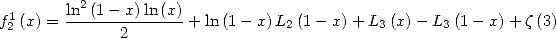(608)

Before carrying on, let us examine this equality. For 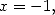the serie defining 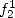converges, but the right hand side of the previous equality does not. However with the formulae by Euler and Landen, we get

The last equality gives us an expression of 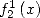valid for . By analytical expansion, we know that the different expression obtained coincide where they are defined simultaneously.
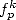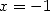We will hence use if necessairy different expressions for the calculations of functions in and .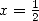

We deduce from the calculation of 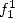that

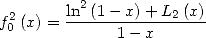(611)

then by integration that

Finaly

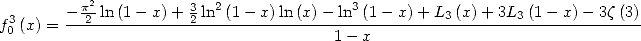(613)

and hence

We deduce from it that

Then by a differentiation calculation, we have

which gives for real

and

and finally

13.3 Applications to the calculation of certain series

We use the previous results with some rightly chosen values for

13.3.1 With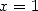

The values are more easily obtained with the Beta functions, for example

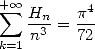(628)

13.3.2 With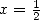

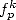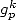We obtain by taking the value of the functions and in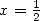

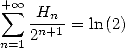(629)

By combining, we get

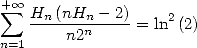(633)

Calculation of 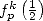for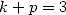

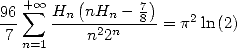(636)

Calculation of 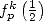for 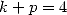To sum up :

We can combine those results and obtain

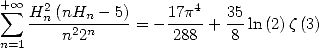(645)

13.3.3 With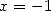

The convergence for the serie is no problems for 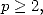we then get

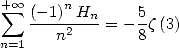(646)

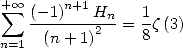(647)

For 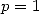we find that

Which gives us

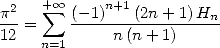(650)

Those equalities are justified because alternating series converges and with of theorem like Tauber, we conclude.
The two following equalities are formally obtained with Maple, they are satisfied numerically but I can  not yet justify them.

which gives by subtracting them and with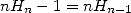

We also have

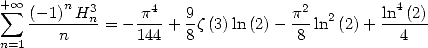(654)

13.3.4 With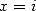

We then get by considering the real and imaginary parts

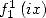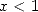The convergence is assured by making for real and by passing through the limit in 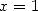with Abel's lemma.

With 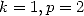We get taking into account the value of 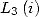and Landen's equality in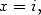

But, we have proved in [12] (calculation of )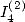

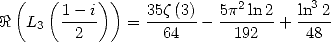(658)

which gives us

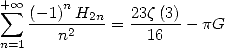(659)

and allows us to find with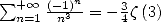

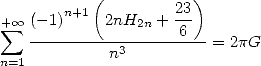(660)

With 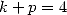The calculations are a bit more complicated, we use this time the equality (658), then the inverse formula for the polylogarithm of order 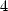which gives

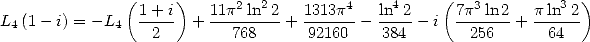(661)

as well as

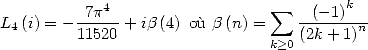(662)

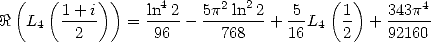(663)

which correspond to the calculation of 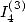in my paper ”formules BBP”, we get

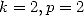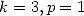We apply the same substitution for and . We then obtain by considering the real part (the imaginary part does not give anything useful)

By combining the different equations obtained, we can deduce

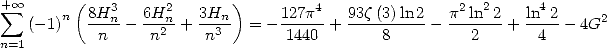(667)

13.3.5 With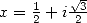

We use in this case the following result.
If we let

(mgl means "multiple by Glaishers” and mcl means ”multiple by Clausen”) then

where 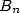is the nth polynomial by Bernoulli.

Then the duplication formula

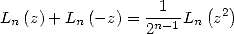(672)

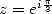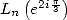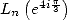with which allows to express and with the help of 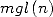and .

Note 25 the calculation of gives the serie

(673)

which can also be written

(674)

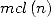We then obtain the following results :

With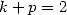

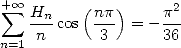(675)

the convergence of this serie is justified by summation in different parts.
We also obtain (under the reservation of convergence, but it is at best very slow that it is hard to check ! ! !)

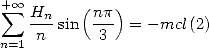(676)

but

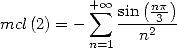(677)

where

or

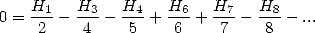(679)

With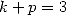

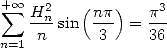(680)

which gives us

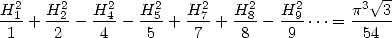(681)

the convergence of this serie is justified by the summation by parts.

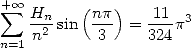(682)

which gives

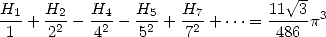(683)

we also have

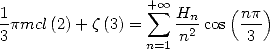(684)

With 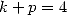we obtain the following formula

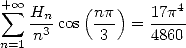(685)

the other make some 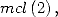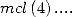intervine
For example

which gives with

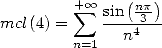(688)

13.3.6 With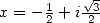

By using the equality

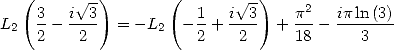(690)

and it's conjugate, we have

whose convegence is assured by packets.

By combining with (675), we obtain

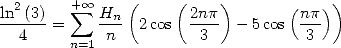(692)

13.3.7 With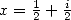

For 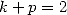We get with 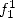the two following formulae which are remarquables

and with 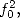the two equality

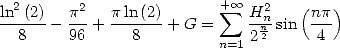(696)

With the functions 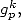we have

With 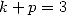The function 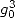gives immediatly

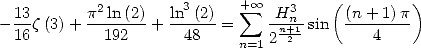(698)

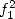and 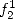gives

13.4 Generalisation

13.4.1 Euler's sums

If we define 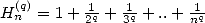(partial sum of 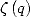), we have Euler's theorem.
If 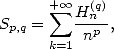then 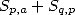is expressed with the help of 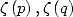and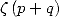

We have some relations with the polylog : 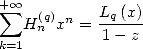. By integrating we have for example

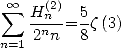(701)

13.4.2 A formula combining Harmonic and combination

Here is a little serie that I've found recently in novembre 2001, mixing the combinations and the sums harmonic ! We can maybe find a more simple proof, but I do find this one quite elegant in the end.

Ok, it's a particular case, I don't know if we can find other series of this kind (and numerically I have yet to find one), but it is maybe worth the effort of searching!

Proposition 26 With and the harmonic sums :
If we let , we get

(702)

Proof. Let 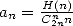. Then

hence

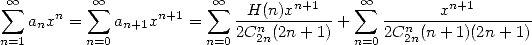(704)

hence in particulae in 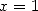and by regrouping the two series containing some 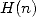, we obtain

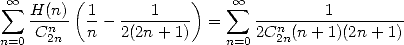(705)

which simplify a bit more the work !

The trick 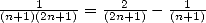unfortunatly does not seem useful because the serie in 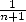is difficult to calculate it seems to me.... Let us find another way.

Note that we hav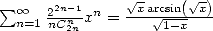e i.e. .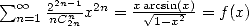

Hence

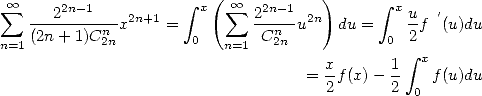
using integration by parts. Hence since using integration by parts, just simply,

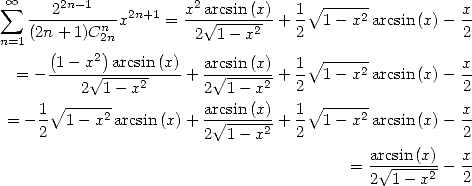
on the convergence radius of ().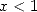

We now need to properly integrate this serie to find a term in  :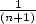

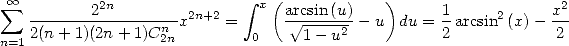(706)

let us add the term for  :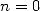

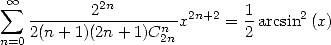(707)

We now use 705 to obtain

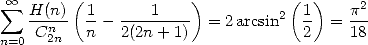(708)

hence finaly

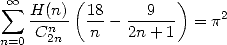(709)

 _

13.4.3 An other formula

We also find some formulae with some special harmonic sums such as Bradley's formula :

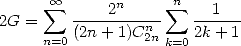(710)

or even this representation of 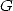which present some troubling similarity with the previous one !

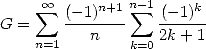(711)

The proof is available in [10].

13.4.4 Harmonics of harmonics !

According to the Gradshteyn [9] (1.516), we can immediatly obtain

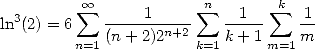(712)