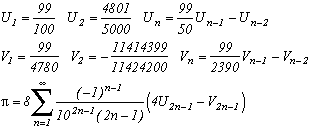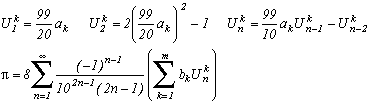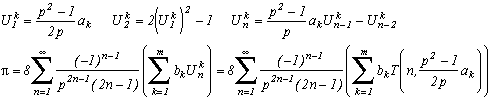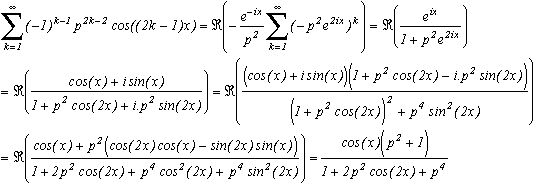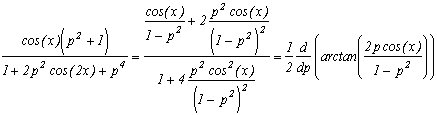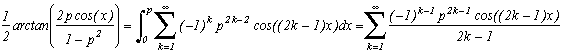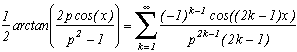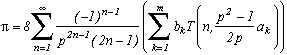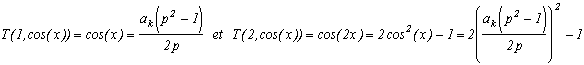Chebyshev's Polynomials, Pi, and the "look BBP"

A first example :

Note that it's a serie with rational terms ! The sequence U_n and V_n are none the other that the value of the Chebyshev's polynomial, respectivaly T(n,99/100) for U_n and T(n,99/4780) for V_n.
And for the more perceptive of you who have already notice a certain similarity between the recurence of U_n and V_n coeffiecent and with the formulae of Arctan (think back to Machin !), well done, here is a more general formula where we use those famous formulae :
If we know a relation of type : then we can construct the sequence U_n^k and the following sequence :
You want something different to 10 as the denominator? Sure, here is a even more general formula for p²>1, still starting from the relation with the Arctan :

with T(n,x) Chebyshev's polynomials.

But where does it originate ?

This algorithm is nearly of the same style as the series of type Machin, but here we allow ourself to have a common denominator of powers (10 in our first example). Those formulae have unfortunatly from the BBP series only the look. Since even if we have at last obtained a 10 in the denominator  instead of 16 from the BBP formula, and that the rest of the sum is rational, it is a function of powers. Indeed, the sequences U_n and V_n are recurrent, therefore we can find the general term under the form U_n=a.r₁ⁿ+b.r₂ⁿ where r₁ and r₂ are the roots of x²-c.x-d=0 such that U_n=c.U_n-1+d.U_n-2. For Delta non zero of course, but go and find me a repeated root ! And even in this case, we write U_n=(a+b.n)rⁿ where r is the repeated root. a and b are found by using U₁ and U₂, but the expressions are so horrible that I prefer not waste any time to write them here. Anyways, as always, there's some roots in the manipulation and we don't even understand how the expression can be rational in the end.
Here again, I have not found this kind of expression on the net, and even the Gradshteyn does not mention it. And yet, it is from this book that the idea came to me and we are finnaly going to see in the proof why I called this page Chebyshev's polynomial and Pi.

Preliminary definition of Chebyshev's polynomials

A little word on Chebyshev (also written Chebychev or Chebyshov) :
Born in 1821 in Okatovo from a noble and cultivated family, he studied at the University of Moscow. His family ruined, he refuse the lecture position that he is offered and lives in poverty until 1847 where he becomes lecturer at Saint-Petersbourg. He then starts to travel and to make the most of his engineer talents, he is in fact very skilled.
On the other hand, he was horrible to his students, he did not like wasting his time, and at the bad habit of stopping his lecture to the second even if in the middle of a sentence, so it is told by "Des mathématiciens de A à Z".
During his carrier, he was mostly interested in number theory and did great progression on the path of proofs for the prime numbers' theorem.

We can define his famous polynomial with degree n with the following relation :
T(n,cos(x))=cos(n.x), T(0,y)=1
In other words, it's the polynomial which allows us to express the cos(n.x) as a function of cos^k(x), kn. It is unique if we choose to make it equal 1 with degree 0 : T(0,y)=1.
Indeed, it checks the following recurrence relation (genius) :

T(n,x)=2x.T(n-1,x)-T(n-2,x)

It's this that will help us to build the sequences U_n^k.

Proof

First of all, we need to make a little preliminary calculation :



How is that going to be any use to us? Well by noting that

we get

(the convergence of the serie is uniform on the whole compact included in [0,1[ and p<1, which justify the reversal of the sum and the integral)
This formula which is recounted in the Gradshteyn/Ryzhik (5th ed. 1.448.6). Working out the proof wasn't that hard, plus you must have noticed that I shamefully did the calculation backward in the first place, since the "by nothing" above is not easy to see straight away!
Then simply replace p by 1/p<1 to find the formula which will use afterwards :

And at this stage, I told myself  "But the cos(n.x), we know them as function of the powers cosⁿ(x) thanks to Chebyshev's polynomial, which if we remind ourself, verify that T(n,cos(x))=cos(n.x).
So we consider the relation . Hence we choose x=x_k such that . (yes, ok, the term inside arccos has to be less than 1, but even if this is not the case, we get a complex x and that work as well in the end with a_k=1...). Note that if the realtion on the arctan is nice, the a_k are rational and thanks to the Chebyshev's polynomials, cos((2k-1)x)=T(2k-1,x) is also.
With this expression, it comes down to :

Now, we're nearly there, we use the recurence of Chebyshev's polynomials' relation to calculate the T(n,x).
Like
  and T(n,x)=2x.T(n-1,x)-T(n-2,x) we then build the final algorithm :



Funny, isn't it ?

Trials

In the case of the first sequence, I had chossen  p=10 and use Machin's formula. Here are the numerical values :

n=2	3,141545
n=5	3,1415926535919
n=10	20 decimals
n=20	41 decimals

We note that the Chebyshev's polynomials' part decrease very slowly since the convergence is nearly of 2n, which is due to the factor 1/10² in the denominator. In my view, it's an interesting alternative solution to the series of type Machin...