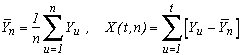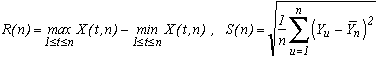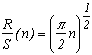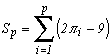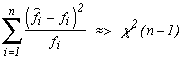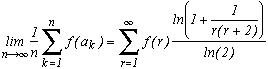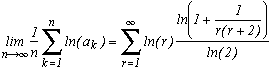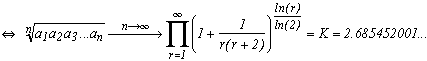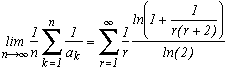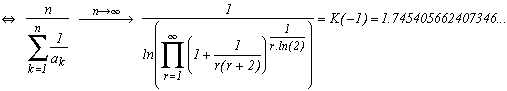|
|
|
|
|
Les décimales de Pi et la statistique
Ce dernier volet de la trilogie de l'aléatoire est consacré aux recherches infatigables pour, ENFIN, trouver quelque chose de particulier à Pi ! Car depuis que l'on s'intéresse à notre constante préférée, et que l'on viole l'intimité de ses décimales jusque-là protégées, il faut bien reconnaitre que cette suite de chiffres, comme sortie de nulle part, intrigue au plus haut point !
D'accord, Pi est irrationnel, on ne retrouvera pas les mêmes séquences périodiquement...
Mais avec quelques outils pas si compliqués, on peut peut-être trouver d'autres motifs ??
Comme les trois autres, cette page a vocation à s'enrichir au fil de ma collecte, et de vos contributions éventuelles !
N'hésitez pas si vous avez quelques idées ou exemples supplémentaires, prévenez-moi...
Voici les paragraphes abordés successivement :
A - La dimension fractale1 - Estimation de la dimension fractale d'une courbe
2 - Méthode de l'échelle réduiteB - Les décimales au fourneau
C - D'autres approches
D - Bibliographie
Bon, après la page sur la théorie de l'aléatoire, il est entendu que l'on ne sait absolument rien sur les décimales de Pi en théorie !
D'accord, mais si l'on regarde les décimales directement maintenant, ne peut-on pas y déceler quelques structures bizarres, qui sortent un peu de l'ordinaire ?
Car tout de même, il doit bien se cacher quelque chose derrière les milliards de décimales que l'on a à disposition ! Comme le disait Gregory Chudnovsky, ce serait une catastrophe si les décimales ne montraient rien avant les 1077 décimales que l'on est capable théoriquement de calculer si l'on utilisait chaque atome de l'univers ! Et l'on en est bien loin, vous imaginez, puisque l'on a simplement passé les 1011 décimales en septembre 2000 (206 milliards).
Les Chudnovsky écrivaient en 1991 que les décimales de Pi apparaissaient plus aléatoire que ce qui serait généré à la main, mais peut-être tout de même pas assez aléatoires !
La loi du logarithme itéré de Chung décrite sur la page consacrée aux phénomènes aléatoires a suggéré à ces mêmes Chudnovsky de considérer une marche aléatoire de séquences de décimales (rappelons qu'avec le théorème de Donsker, une somme de marches aléatoires converge en gros vers un mouvement Brownien). A partir de là, on peut construire des objets fractales à partir des décimales de Pi, et pourquoi pas mesurer leurs dimension fractale ! Ben oui, ça c'est une bonne idée !
La dimension fractale d'un processus classique comme le mouvement Brownien est 1.5.
Vanouplines, de la Vrije Universiteit te Brussel (Belgique), a montré que la dimension de Pi est elle aussi très proche de 1.5.
Les fractales sont un très riche domaine des mathématiques, et ma page sur Mandelbrot indiquait que l'on pouvait même trouver Pi dans l'ensemble de Mandelbrot !
La définition d'un fractale, donnée par Mandelbrot lui-même dans son livre "The fractal geometry of nature" (1983) est, comme le dirait Weyl du "brouillard dans le brouillard" ! :Un objet fractale est par définition un objet dont la dimension de Hausdorff-Besicovitch est strictement supérieure à la dimension topologique"
hum, merci...
Mandelbrot indique d'ailleurs un peu plus loin qu'il continue à penser que ce serait mieux sans définition... :-)
Côté dimension, la chose est un peu plus intuitive dans les espaces euclidiens : un point est bien sûr de dimension 0, une ligne est de dimension 1, un plan est de dimension 2, un volume de dimension 3, etc...
Seulement, ces dimensions sont entières... Peut-on imaginer des courbes de dimension rationnelle, voire réelle ?
En fait, de manière intuitive le plan est rempli d'une infinité de lignes. La ligne est d'épaisseur nulle, mais si on lui faisait prendre des virages dans tout les sens, et de plus en plus serrés, la ligne commencerait à occuper beaucoup d'espace, et c'est alors que sa dimension fractale dépasse 1, la limite étant donc le plan de dimension 2. Bref, plus la courbe est heurtée, et ceci à n'importe quel zoom, plus la dimension de la courbe sera supérieure à 1.
A.1 - Estimation de la dimension fractale d'une courbe
On utilise ici la méthode "box count" qui repose sur la seconde définition de Mandelbrot d'un objet fractal, toute aussi vague, mais plus intuitive :Un objet fractal est une forme faite de parties similaires à l'ensemble.
Bref, de n'importe quelle échelle, l'objet fractale nous apparaît toujours de la même façon...
Prenons une côte sur une carte maritime... voilà un joli exemple de courbe fractale !
Bon, on se munit de papier millimétré de cases d'un millimètre de large, puis de papier de cases de 2 millimètres de large, de 4mm, et 8mm de large aussi. Vous l'avez compris, les tailles différentes de carrés servent à comparer le dessin à différentes échelles... C'est la cohérence de la forme aux différents zooms utilisés qui détermine le degré de complexité fractale d'un objet.
On prend pour chacun des papiers millimétrés une même zone rectangulaire et on la plaque ensuite sur le dessin côtier. On compte alors le nombre de carrés traversés par la courbe et on reporte cela dans un tableau du type de celui qui suit : (données fictives tirées de [6])
Taille des carrés
Nombre de carrés traversés
Taille des carrés*Nombre de carrés traversés
(longueur de la côté)Logarithme décimal de la taille des carrés
Logarithme de la taille de la côté
Dimension fractale
1
6998
6998
0
3.845
1.39
2
2679
5358
0.301
3.729
1.35
4
1054
4216
0.602
3.625
1.32
8
424
3392
0.903
3.530
1.31
16
171
2736
1.204
3.437
1.33
32
68
2176
1.505
3.338
1.33
64
27
1728
1.806
3.238
1.44
128
10
1280
2.107
3.107
La longueur de la côte est plus élevée lorsque la précision est grande car on décèle alors plus de virages sur la côte. On voit alors que l'objet ne peut être d'une dimension fractale élevée, cependant celle-ci n'est pas non plus 1.
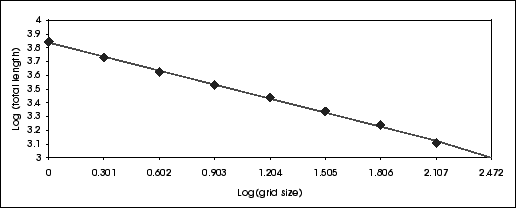
En traçant le logarithme de la taille de la côte (5e colonne) en fonction du logarithme de la taille des carrés, on obtient une droite de régression dont la pente est 1 - D, où D est la dimension fractale. Intuitivement, cela se comprend. En effet, si la pente était de 1, la taille de la côte serait proportionnelle à la précision souhaitée, donc il n'y aurait aucun caractère fractal dans cette courbe et D=0 dans ce cas. Ici, la pente est négative comme le montre la figure suivante, ce qui signifie que la taille des carrés augmente plus vite que la taille visible de la côte ne décroît. Dans le tableau ci-dessus, la dimension est évaluée pour chaque pente entre deux points.
Avec une pente de -0.339 de la droite de régression, on obtient une dimension fractale moyenne de D=1-(-0.339)=1.339.
Bon, maintenant que l'on sait ce qu'est une dimension fractale, l'idée est de tracer la marche aléatoire des décimales de Pi et d'estimer sa dimension fractale.
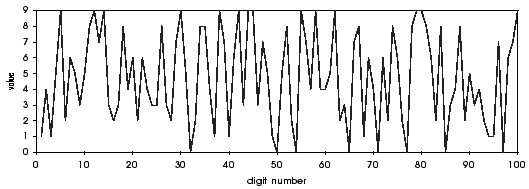
Voici le graphique où chaque décimale est reliée à la précédente et à la suivante par une ligne :
D'accord, mais il y a tout de même un sacré problème.... C'est que dans le cas de la côte maritime, l'échelle était la même en abcisse et ordonnée. Ici, ce n'est plus du tout le cas.... aïe !
A.2 - Méthode de l'échelle réduite
Mais nos amis les mathématiciens ont réfléchi à ce problème et ont sorti la méthode de "l'échelle réduite" si l'on peut dire (rescaled range) dans les années 60 avec Hurst, Mandelbrot et Wallis.
Hurst a posé les notations suivantes :
où Yi est la ie décimale de Pi-3.
Il définit ensuite les deux statistiques :
Et le plus fort, c'est que l'ami Hurst a remarqué que la statistique R/S prenait souvent une forme remarquable ! De manière empirique, on obtient :
où c est une constante souvent prise égale à 1/2 et H est l'exposant de Hurst. Ceci permet de garder l'échelle de l'abscisse et de réduire les observations des sommes cumulées des décimales selon cette échelle.
Mais comment raccrocher à la dimension fractale ?
Et bien en fait, la relation entre la dimension fractale D et le coefficient de Hurst H estD=2-H
Ceci se comprend intuitivement puisque plus H est élevé, plus le rapport R/S augmente rapidement avec n. Ceci signifie que l'amplitude maximale augmente de plus en plus vite par rapport à la variation, ou plus prosaïquement que la variation augmente moins vite que l'amplitude maximale. Mais ceci n'est rien d'autre (pour moi !) que le fait que l'on a "zoomé" sur la courbe mais que la variation n'a pas suivi, et donc que la dimension fractale décroit.
Toujours avec les mains, un exposant H entre 0.5 et 1 montre des signes de persistence dans la courbe, c'est-à-dire que si elle a connu une croissance sur une période, celle-ci continuera probablement la période suivante. Pour des exposants inférieurs à 0.5 c'est exactement l'inverse avec des agitations plus chaotiques et moins prévisibles, ceci étant logique puisque la dimension fractale augmente alors. Il n'est donc pas étonnant que pour des processus indépendants de variance finie, cet exposant H soit de 1/2, (par exemple pour les mouvements Browniens, ce qui montre en passant que leur dimension fractale est 1.5).
D'ailleurs, et c'est très fort de retrouver encore Pi dans ce coin, Feder a montré en 1988 que pour ces processus, on a exactement :
Incroyable, non ??
Pour la plupart des phénomènes naturels, H=0.72 soit D=1.28.
Et pour notre ami Pi maintenant ?
Plutôt que les décimales de Pi elles-mêmes, la moyenne cumulée des décimales est une courbe plus "continue", qui ressemble plus à un processus aléatoire. En notantla ie décimale de Pi, on considère donc le processus :
étant entendu que bien sûr avec des digits entre 0 et 9, la moyenne attendue est 4.5 et donc 2
-9 devrait être proche de zéro en moyenne.
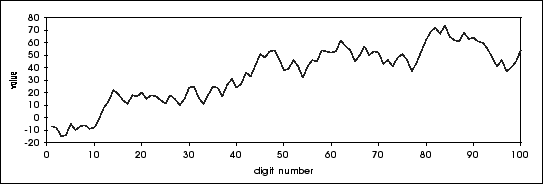
En fait, sur les 100 premières décimales, on obtient le graphique suivant de Sp :
Ben cela, si c'est pas du beau processus ?!
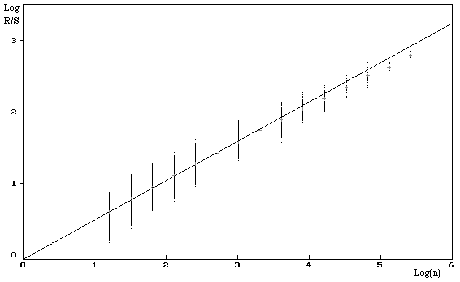
Pour 1.25 million de décimales, on obtient la courbe suivante de la dimension fractale (assortie d'intervalles de confiance) :
Une tendance claire, qui fournit par la pente la dimension fractale de 1.45. Eh oui, ce n'est pas un processus à accroissements totalement indépendants comme le mouvement Brownien ! Il existe une petite persistence (H=0.55), mais de là à trouver laquelle... hmmm...
Bref, tout la dimension fractale est un bon indicateur pour nous dire que visiblement, quelque chose ne va pas ! Mais cela ne nous dit pas quoi... Examinons donc un peu la répartition empirique des décimales :
Le fait que les décimales de Pi traversent sans encombres les tests les plus classiques comme ceux du Khi2, des mains de poker, de la loi de l'arctan n'arrange pas les choses...
Euh.... mais qu'est-ce que tout ceci au fait ?
Bon, en fait les mathématiciens n'ont pas trouvé grand chose - ce n'est pas un reproche ! :-) - sur la répartition des décimales en étudiant le nombre Pi lui-même, à travers sa place dans les formules ou théories... La démarche non plus probabiliste mais statistique consistait donc à inverser la méthode et partir cette fois-ci des décimales pour trouver des singularités propres à Pi. Et force est de constater que ce n'est pas simple...
C'est le test le plus classique, et un des plus faibles... les statisticiens ont l'habitude de dire que tout passe avec un Khi2 :-)
C'est une statistique qui calcule la somme des écarts au carré des fréquences observées et des fréquences attendues. Sous l'hypothèse que les données suivent effectivement les répartitions attendues, elle suit comme son nom l'indique un Khi2 à n-1 degrés de liberté où n est le nombre de fréquences que l'on considère :
fi est la fréquence attendue et
On n'a pas n degrés de liberté puisque la dernière fréquence est forcément connue grâce aux autres (la somme des fréquences est le nombre de décimales utilisées, donc est connue !). Seules n-1 fréquences influencent donc véritablement le calcul de la statistique c'est pourquoi on attribue n-1 degrés de liberté à la loi. Tout ceci se démontre bien sûr, mais ce n'est pas l'objet de cette page ni de ce site !
Il suffit ensuite de comparer la valeur obtenue aux valeurs prises par la loi associée. Si cette valeur est inférieure au fractile d'ordre 0.95, cela signifiera que la probabilité d'observer dans dans la nature une valeur du Khi-deux supérieure à cette statistique est supérieure à 5%, etc... Bref, cela impliquerait que notre constante n'a rien
d'exceptionnelle...
Et devinez ce qui se passe !
Ben oui, rien.... :-)
Voici les fréquences observées pour les 200 premiers milliards de décimales de Pi-3 :
Chiffre Apparitions dans Pi Apparitions dans 1/Pi 0 20000030841
19999945794
1 19999914711
20000122770
2 20000136978
20000060451
3 20000069393
20000182235
4 19999921691
19999876817
5 19999917053
19999977273
6 19999881515
19999911742
7 19999967594
20000001035
8 20000291044
19999927489
9 19999869180
19999994394
Statistique du Khi-deux 8.09
4.18
Ces deux statistiques correspondent respectivement à des fractiles d'ordre 0.53 et 0.9. C'est-à-dire que l'on a respectivement 53% et 90% d'observer dans la nature des statistiques prenant des valeurs plus élevées... Bref, rien d'exceptionnel donc !
Notons que ces deux statistiques sont calculées uniquement sur les 200 milliards de décimales, donc c'est vraiment pour observer si quelque chose ne va pas du tout ! Car il pourrait y avoir des petites variations et il n'y a aucune raison qu'une décimale apparaisse plus que les autres, ou moins. Ce n'est donc pas très puissant !
Kanada, qui a calculé ces 200 milliards de décimales, a effectué les tests par tranches de décimales, les fichiers sont disponibles à l'adresse ftp://pi.super-computing.org/. Le test du Khi2 pour des divisions successives en 10 blocs parmi 6 milliards de décimales est disponible en local. Mais rien de vraiment spécial...
Bon, continuons notre investigation !
Cette statistique est un peu plus fine que le Khi-deux puisqu'elle s'intéresse non plus à chaque décimale, mais aux combinaisons entre décimales.
On découpe les décimales par blocs de 5, et dans chacun de ces blocs, on regarde quelle combinaison du poker on trouve.
Pour un bloc, on tire forcément soit des décimales différentes, ou une paire, un brelan, une double paire, un carré, une quinte (euh, dur au poker !), ou un full...
Ce genre de test peut paraitre plus amusant que sérieux ! Cependant, dans la nature on s'attend à trouver un certain nombre de paires, de brelans, etc... Ceci teste donc à un niveau supérieur au Khi-deux la régularité des fréquences des combinaisons de décimales.
Pour 200 000 mains de poker par exemple, les fréquences attendues sont les suivanets :
Combinaisons Fréquences attendues Décimales différentes
ABCDE60480
Paires
AABCD100800
2 Paires
AABBC21600
Brelans
AAABC14400
Full House
AAABB1800
Carré
AAAAB900
Quinte
AAAAA20
Total 200000
Pour obtenir ces fréquences attendues, il suffit de dénombrer les cas possibles sur les cas favorables comme on dit en proba. Prenons un exemple avec le carré :
on a 1 chance sur 10 de tirer exactement A (10 décimales), une autre chance sur 10 de tirer encore A et ainsi de suite, donc en continuant, on a 1/104 chances de tirer AAAA. Mais cela pourrait être A comme C ou un autrre chiffre, donc on a 10 cas possibles, on multiplie le total par 10, ce la donne 1/103. Ensuite, il faut tirer un autre chiffre que celui représenté par A, il y en a plus que 9, donc on a 9 chances sur 10 de bien tomber et l'on multiplie donc le total par 9/10. Enfin, il faut placer ce B parmi les A, comme il y a 5 places, on a 5 choix possibles et l'on multiplie donc le tout par 5.
On obtient au final :5*9/(10*103)=0.0045
Comme on a 200 000 tirages, le nombre de carrés attendus est 200 000*0.0045=900, c'est bien ce qui était attendu. En y allant méthodiquement (bref pas trop comme moi !), on doit toujours y arriver, mais il est vrai que ce n'est pas trop facile et qu'il faut un certain entrainement !
Le principe consiste ensuite à effectuer un test du Khi-deux sur les résultats pour les comparer aux fréquences attendues. L'équipe de Kanada a effectué ces divers tests sur le record à 6 milliards de décimales. On regroupe en général le carré et la quinte à cause de la faible fréquence de la quinte, mais cela n'a pas été fait dans le test suivant. Le Khi2 considéré a donc 6 degrés de liberté, et l'on a bien sûr fait 1 200 000 blocs de 5 décimales :
DECIMALE 1 2 3 4 5 6 7 8 9 10| TOTAL ATTENDU ---------------------------------------------------------------------------------------------------------------------------------------------- Déc diff 36294173 36290069 36290127 36286820 36290298 36289575 36294505 36289984 36281969 36282987| 362890507 362879996.98 Paires 60475840 60476864 60485069 60484354 60477375 60474120 60476577 60473797 60485057 60486104| 604795157 604799994.96 2 Paires 12956498 12958229 12954176 12962149 12961317 12963422 12962341 12963379 12959383 12960093| 129600987 129599998.92 Brelan 8643856 8641687 8639415 8636938 8640244 8639352 8635473 8640375 8642190 8641230| 86400760 86399999.28 Full House 1078694 1080546 1079458 1079213 1079216 1080368 1078612 1080174 1078744 1078985| 10794010 10799999.91 Carré 539027 540460 539627 538583 539598 541309 540416 540236 540532 538638| 5398426 5399999.95 Quinte 11912 12145 12128 11943 11952 11854 12076 12055 12125 11963| 120153 120000.00 ---------------------------------------------------------------------------------------------------------------------------------------------- KHI2 7.98 3.27 5.10 6.36 1.46 6.67 6.74 2.03 5.30 5.99| 4.33 (FRACTILE 0.25 0.77 0.54 0.4 0.96 0.36 0.35 0.92 0.51 0.44| 0.64 APPROCHE)
Il y a donc eu un test par décimale, puis un test total (c'est pratique le Khi2 pour cela, on peut tester n'importe quoi !). Et l'on voit bien qu'il n'y a rien à signaler, aucun fractile ne s'approchant vraiment de 0.05...
Tout au plus les écarts pour la décimale 5 sont jugés un peu trop faibles ! :-)
Aïe aïe aïe, ça se complique, toujours rien...
Mais continuons !
B.3 - Test des sommes de 5 décimales
Comme son nom l'indique, ce test découpe les décimales par 5 et calcule pour chacun de ces blocs la somme. Ce test est censé mettre en valeur des parties où par exemple de plus fréquentes apparitions de hautes décimales provoquerait des sommes plus élevées que dans la nature, etc...
Les résultats attendus sont des réalisations de lois multinômiales. Mais il me semble plus simple de retrouver les résultats par un bon raisonnement logique...
Vous savez que l'on estime une probabilité par le nombre de cas favorables sur le nombre de cas possibles. C'est ici une manière de procéder.
Commençons simple : prenons un bloc de 5 chiffres, pour que leur somme fasse 0, il faut que les 5 fassent 0, il y a donc une seule possibilité ! C'est le nombre de cas favorables. D'autre part, chacun des 5 chiffres a 10 valeurs possibles, le nombre de cas possibles est donc 10*10*10*10*10=105. Donc la probabilité que la somme fasse 0 est 1/105. Comme l'on a ici 1.2 milliards de blocs, cela donne1.2*109/105=12000
cas attendus tout simplement.
Allez, un deuxième exemple un peu moins trivial car je sens que vous êtes chauds !
Dans le troisième cas, il faut somme des 5 chiffres valant 2. Donc on a une disjonction de cas :
Soit deux chiffres valent 1 et l'on a C(5,2)=10 (combinaisons de 2 parmi 5, C(n,p)=n!/(p!(n-p)!) ) manières de les choisir parmi les 5. En passant par une loi multinomiale M(5,0.1,0.1,...) on obtient 5!/(3!2!0!0!...)*1/(103102100100...)=10/105 la proba de cet événement, pour les connaissseurs qui veulent aller vite.
Soit un chiffre vaut 2 et les quatre autres valent 0, cela représente 5 cas possibles suivant la place du 2. Avec la multinomiale, 5!/(4!1!0!0!...)*1/(104101100100...)=5/105 est la proba de cet événement. Au final, on a 15 cas possibles soit une probabilité de cet événement de 15/105 que l'on retrouve par les deux méthodes à la main ou par la multinomiale.
Le nombre attendu de "SUM=2" sur 1.2 milliards de blocs est donc1.2*109*15/105=180000
Je vous assure que c'est vite amusant de savoir si l'on a un tout petit peu de logique de dénombrement, essayez !
Toujours sur l'échantillon de 6 milliards de décimales et en découpant en blocs de 600 millions de décimales, l'équipe de Kanada a obtenu les résultats suivants :BLOC = 1 2 3 4 5 6 7 8 9 10| TOTAL ATTENDU ------------------------------------------------------------------------------------------------------------------------------------------------ SUM= 0 1216 1197 1193 1250 1200 1176 1196 1214 1152 1233| 12027 12000.000 SUM= 1 5923 6023 5957 5967 6017 6028 6077 6045 6047 5975| 60059 60000.000 SUM= 2 17848 18002 17896 17914 18100 17835 17874 18127 17887 17937| 179420 179999.998 SUM= 3 42128 41943 41885 42180 41659 41987 41697 42120 41935 42088| 419622 419999.997 SUM= 4 84093 83998 83899 83694 83827 84749 83906 84146 83647 82995| 838954 839999.993 SUM= 5 150933 151285 152040 150889 150914 151440 151465 151357 151106 150406| 1511835 1511999.987 SUM= 6 252052 251554 252425 252377 251639 251762 251674 252596 252215 252220| 2520514 2519999.979 SUM= 7 395189 396146 395922 396137 396044 395779 396032 396210 396185 395973| 3959617 3959999.967 SUM= 8 593637 592684 593729 594333 593971 593748 594449 594366 595328 593856| 5940101 5939999.951 SUM= 9 858470 858342 858321 856921 858350 859226 857611 857056 857478 858960| 8580735 8579999.929 SUM= 10 1194437 1195429 1194514 1194536 1193553 1194870 1194976 1194134 1193540 1194598| 11944587 11951999.900 SUM= 11 1605266 1607515 1608231 1607348 1608394 1605279 1609486 1608762 1609340 1609442| 16079063 16079999.866 SUM= 12 2091618 2095708 2094196 2092715 2093180 2091291 2095945 2093030 2093830 2092915| 20934428 20939999.826 SUM= 13 2648030 2646321 2645322 2643188 2647514 2646881 2644930 2645962 2643577 2643418| 26455143 26459999.780 SUM= 14 3252283 3252822 3249652 3253274 3250272 3253381 3249525 3252776 3253078 3250408| 32517471 32519999.729 SUM= 15 3899546 3898175 3893160 3893092 3898171 3894389 3895990 3897963 3895193 3892981| 38958660 38951999.675 SUM= 16 4551996 4551347 4554651 4553603 4553925 4552191 4556515 4553971 4552146 4553568| 45533913 45539999.621 SUM= 17 5201733 5201032 5201711 5203465 5201273 5206295 5205467 5202503 5205968 5204304| 52033751 52019999.566 SUM= 18 5809804 5806104 5812753 5808793 5810430 5805164 5806757 5809698 5808856 5811122| 58089481 58079999.516 SUM= 19 6335116 6335295 6334714 6340044 6337456 6338388 6334646 6335387 6333802 6337037| 63361885 63359999.472 SUM= 20 6753880 6755164 6757793 6756423 6757089 6754552 6754976 6757225 6758836 6754169| 67560107 67571999.437 SUM= 21 7048473 7047684 7054697 7049417 7047712 7050818 7055967 7052409 7047565 7049867| 70504609 70499999.413 SUM= 22 7195837 7204989 7194831 7199905 7198519 7203840 7196208 7201386 7198388 7201909| 71995812 71999999.400 SUM= 23 7203470 7201800 7195852 7197458 7200117 7198749 7199849 7195443 7198608 7197627| 71988973 71999999.400 SUM= 24 7050060 7047213 7049745 7048952 7051751 7051705 7051021 7045667 7046796 7052240| 70495150 70499999.413 SUM= 25 6761856 6760420 6761986 6763441 6754330 6755526 6758730 6761985 6763792 6756381| 67598447 67571999.437 SUM= 26 6335540 6335738 6337255 6332486 6337542 6333532 6337991 6336563 6336177 6338455| 63361279 63359999.472 SUM= 27 5808627 5808453 5807373 5807508 5808064 5810369 5804582 5805840 5805965 5810139| 58076920 58079999.516 SUM= 28 5202613 5202126 5204017 5200678 5197496 5202708 5204795 5201079 5205991 5202461| 52023964 52019999.566 SUM= 29 4555210 4553387 4553230 4555919 4557110 4552793 4553511 4554100 4554409 4553357| 45543026 45539999.621 SUM= 30 3895961 3892915 3894162 3894606 3894262 3894426 3892307 3894606 3894956 3895352| 38943553 38951999.675 SUM= 31 3256018 3250243 3251867 3249837 3253079 3249265 3253032 3249406 3252452 3253948| 32519147 32519999.729 SUM= 32 2644512 2648978 2647511 2648128 2643971 2644766 2643985 2645457 2645607 2644185| 26457100 26459999.780 SUM= 33 2093395 2095113 2096225 2095226 2092831 2094830 2093681 2095801 2093199 2095237| 20945538 20939999.826 SUM= 34 1607321 1609097 1608165 1609658 1608917 1608961 1606667 1607598 1608289 1608217| 16082890 16079999.866 SUM= 35 1195598 1193679 1193808 1195018 1196316 1196777 1195415 1195170 1195168 1193806| 11950755 11951999.900 SUM= 36 857619 858681 856824 858062 858473 859108 856967 857623 856698 857784| 8577839 8579999.929 SUM= 37 594438 594375 594600 593669 594880 595027 594359 594477 594675 593578| 5944078 5939999.951 SUM= 38 394990 395440 395415 397078 396760 396359 395443 396010 395884 395526| 3958905 3959999.967 SUM= 39 251920 251551 251452 252773 252682 252077 251600 252275 252268 251785| 2520383 2519999.979 SUM= 40 150416 151017 150658 150839 150496 150787 151427 151874 150468 151099| 1509081 1511999.987 SUM= 41 83539 84096 83381 84021 83994 84005 84573 83593 84225 84090| 839517 839999.993 SUM= 42 42301 41678 41976 42218 42204 41926 41479 41954 42097 42034| 419867 419999.997 SUM= 43 17972 18008 17838 17777 18371 17881 18101 17928 17898 18073| 179847 179999.998 SUM= 44 5958 6047 5932 5986 5964 6105 5937 5930 6026 6029| 59914 60000.000 SUM= 45 1158 1186 1236 1197 1181 1249 1179 1178 1253 1216| 12033 12000.000
Hum, rien de particulier encore... désespérant...
L'équipe de Kanada a effectué un test supplémentaire, qui s'appelle le "Gap test" (test des écarts) mais que je n'ai jamais compris ! Si quelqu'un veut bien m'éclairer ? Le fichier qui en rend compte est situé à cette adresse.
Le test de la loi de l'arctan reste également un mystère pour moi et je n'ai pas trouvé de référence sur le web qui en discute. Donc comme on ne peut pas tout inventer soi-même (!), je m'incline, j'attendrai qu'une âme charitable vienne à mon secours...
Signalons encore que de nombreuses méthodes graphiques ont été utilisées pour tenter de trouver des régularités dans les décimales. Par exemple transcrire les décimales en binaire et les mettre bout à bout dans un carré pour constituer une image. Si les paysages formés semblent plus réguliers que ceux qui seraient formés par le hasard pur, les Chudnovsky n'ont pas trouvé d'explication satisfaisante à ce genre de phénomènes...
Voilà pour un rapide tour d'horizon des méthodes statistiques très classiques d'analyse des décimales
Bien des idées farfelues ont transité dans le domaine de la recherche de singularités. Quelques idées parfois méritent le détour, comme celle qui consiste à utiliser les connaissances sur un groupe de nombres en général pour tester l'appartenance à ce groupe d'une constante en particulier. Un bon exemple concerne la constante de Khintchine.
Aleksandr Khintchine fait paraître en 1935 un petit recueil sur les fractions continues, ("Continued Fractions", pourquoi faire compliqué ?) dans lequel il remarque que la moyenne géométrique des coefficients d'une fraction continue tend vers une certaine constante, et ceci presque sûrement, (sauf un pour un ensemble de nombres de mesure nulle, la mesure étant celle de Lebesgue)...
En français et en gros (car ce site n'est pas un cours de théorie de la mesure !), cela signifie que pour ce résultat est vrai sauf pour un ensemble de nombres isolés, sans continuité entre eux, même de taille infinie (comme N ou Q). Il existe bien sûr quelques ensembles exotiques qui ne rentreraient pas dans cette explication intuitive mais là n'est pas l'intérêt.
Plus généralement, il montre le théorème suivant :
Théorème de Khintchine
Supposons que f(r) soit une fonction positive d'un entier r et supposons qu'il existe deux constantes positives C et d telles que
En d'autres termes, f doit croître moins vite que la racine carrée.
Alors, alors pour presque tous les nombres de l'intervalle [0,1], en notant ak les coefficients de leur fraction continue régulière, on a l'égalité suivante :
La démonstration de ce théorème, qui occupe plusieurs pages du bouquin de Khintchine, me parait un peu ambitieuse pour l'objet de ce site, mais si un jour j'ai un peu de courage, je la retranscrirai peut-être !
Il en existe d'autres versions basées par exemple sur la théorie ergodique, ce qui ne semble pas très étonnant vu la forme du résultat et son caractère presque-sûr.
On peut déjà observer que la condition sur f est suffisante pour assurer la convergence du membre de droite dont le terme de la série est équivalent à l'infini à f(r)/r2.
On prend maintenant une fonction f qui satisfait l'hypothèse du théorème, à savoir le logarithme.
On obtient alors que pour presque tous les nombres dans [0,1] :
Et voici apparue la célèbre constante de Khintchine... Elle est assez passionnante d'ailleurs, mais bon si l'on commence à s'enflammer de tous les côtés, on n'en finira plus ! Voir tout de même les références de la bibliographie pour en savoir un tout petit peu plus.
Pas facile à calculer avec cette expression. Mais Bailey, Borwein et Crandall ont récemment obtenu tout de même 7350 décimales de K à l'aide de séries de fonctions Zêta qui convergent nettement plus vite.
On peut aussi obtenir une formule avec la moyenne harmonique et f(r)=r-1 :
On pourrait obtenir aussi un K(-2) en prenant f(r)=r-2 etc....
Cette deuxième formule pour la moyenne harmonique est également un résultat "presque sûr", donc un petit ensemble de nombres ("négligeable" au sens des probabilités) ne vérifie pas cette formule. D'accord, toutes les fractions avec des suites de coefficients très simplement définissables feront partie de cet ensemble négligeable (pensons à la constante e par exemple, ou le nombre d'or, qui trivialement ne vérifient pas les deux formules de moyenne géométrique ou harmonique)... mais quelle est la forme de l'ensemble des suites telles que la moyenne géométrique ne tend pas vers l'expression considérée ? C'est une simple question d'analyse, non ?
Et même si l'on sait que les nombres qui ne suivent pas ce résultat sont extrêmement peu nombreux, l'idée consiste à vérifier si les coefficients de la fraction continue de Pi suivent bien ce résultat.
En tous les cas, encore une façon de chercher un groupe particulier dans lequel ranger Pi. Le cerner d'une manière ou d'une autre !
David Bailey dit à ce propos que les coefficients de la fraction continue de Pi ne semblent pas présenter de motif particulier et sont supposés être aléatoires en un certain sens.
On connait aujourd'hui 17 001 303 coefficients de la fraction continue de Pi dont les premiers sont Pi = [3; 7; 15; 1; 292; 1; 1; 1; 2; 1; 3; ...]. La moyenne géométrique de ces coefficients est 2.686393 et la moyenne harmonique 1.745882. Elles s'approchent effectivement de ces constantes K et K(-1) même si le calcul ne s'est effectué que sur 17 millions de coefficients, ce qui est bien peu à l'échelle de l'infini !
Donc là encore, aucune conclusion tangible ne peut être tirée...
On le voit avec la constante de Khintchine, au détour de théories passionnantes sur le comportement général des nombres, les mathématiciens sont tentés d'observer si Pi se comporte de manière particulière. Les outils de l'étude statistique des décimales étant bien limités et n'ayant en fait pas donné grand chose, c'est une nouvelle approche assez intéressante.
La quête des décimales n'apportera sans doute pas grand chose à cette étude paradoxalement car il n'y a aucune raison pour qu'à partir de 207 milliards de décimales, tout à coup on trouve un motif très particulier qui nous saute aux nez !! C'est encore le rêve de beaucoup de mathématiciens après tout, alors on ne sait jamais...
Mais le motif est déjà probablement devant nos yeux pourtant grands ouverts, mais sans doute pas encore assez, ou bien il n'existe pas et on ne le saura sans doute que si l'on démontre un résultat très fort comme la normalité des décimales de Pi. Et encore, Pi ne serait pas Pi sans SES propres décimales, et pas une de différente ! La normalité n'est donc pas tout, elle ne banalise pas complètement et définitivement le nombre.
Pareil en ce qui concerne la représentation de Pi en fraction continue. Mais cette idée de représentation est intéressante. On a vu avec l'algorithme compte-goutte qu'il existe des bases où Pi est un des nombres les plus simples, c'est-à-dire remarquable ! Plus on trouvera de manière de représenter les nombres et des classes de nombres associées à ces représentations, plus l'idée que l'on aura de Pi et de sa place parmi les nombres sera précise. C'est donc un domaine à mon avis encore très ouvert...
4 références de référence !
[1] Laboratoire de Kanada, Archives de Pi - Super-computing.org
ftp://pi.super-computing.org/
[2] Patrick Vanouplines, Université libre de Bruxelles, Rescaled range analysis and the fractal dimension of Pi.
http://gopher.ulb.ac.be/~pvouplin/pi/pi.ps
[3] D. Bailey, J. Borwein , R. Crandall, On the Khintchine Constant
http://www.nas.nasa.gov/Research/Reports/Techreports/1997/PDF/nas-97-030.pdf
[4] "La constante de Khintchine", miroir basé à l'Inria du site de Steven Finch
http://pauillac.inria.fr/algo/bsolve/constant/khntchn/khntchn.html
retour à la page d'accueil