4 Formule de type Machin

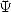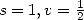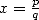Par rapport à la fonction , c’est le cas où ses paramètres valent , et varie.

La fonction Arctan s’exprime de cette manière avec la fonction 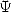. Ainsi, on a

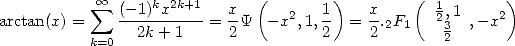(27)

Ceci signifie que les formules d’Arctan type Machin s’expriment comme combinaison linéaire de la fonction 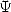. Par exemple, on a d’après la formule d’Euler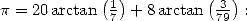

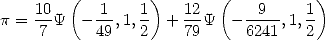(Euler)

On a affaire ici à des séries rationnelles qui ont constitué la principale manière de calculer Pi entre leur découverte ”officielle” par Machin (1705) et celle des algorithmes modernes de type Brent-Salamin / Borwein à la fin des années 70.

Cette formule correspond en notation hypergéométrique à la forme

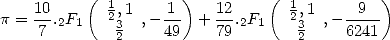(28)

Les démonstrations s’effectuent en utilisant la formule

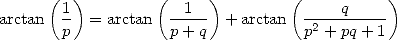(29)

plusieurs fois. C’est lourd, autant le dire ! Une méthode simple a été élaborée par les Borwein en 1987, qui consiste à montrer qu’une formule

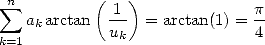(30)

est équivalente à l’expression complexe

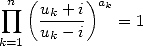(31)

A partir de là, les preuves des formules d’arctan deviennent aussi simple qu’un produit de nombres complexes !