|
|
|
|
|

Calcul des décimales de Pi : du neuf avec du vieux !
Résumé
En exploitant une idée géométrique très simple, Benoît, toujours aussi prolifique, améliore l’efficacité de la méthode d’Archimède pour le calcul des décimales de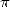 .
Cette approche mélange algorithme et série et permet en théorie d’obtenir une vitesse
de convergence aussi grande que l’on veut. La convergence reste cependant
linéaire.
.
Cette approche mélange algorithme et série et permet en théorie d’obtenir une vitesse
de convergence aussi grande que l’on veut. La convergence reste cependant
linéaire.
1 La Formule
Une version moderne de l’algorithme d’Archimède consiste à définir l’algorithme
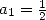 et
et
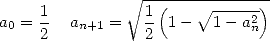 | (1) |
qui permet de calculer 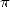 étant donné que
étant donné que
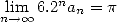 | (2) |
L’efficacité de la méthode n’est pas mauvaise car la convergence est en 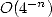 . Elle
n’est pas extraordinaire non plus et de nombreuses autres méthodes (algorithmes,
séries..) convergeant aussi linéairement, l’égalent ou la supplantent (sans compter
bien sûr les algorithmes de Salamin-Brent ou autres frères Borwein). Nous proposons
tout de même de partir de cette vieille idée et de calculer les décimales de
. Elle
n’est pas extraordinaire non plus et de nombreuses autres méthodes (algorithmes,
séries..) convergeant aussi linéairement, l’égalent ou la supplantent (sans compter
bien sûr les algorithmes de Salamin-Brent ou autres frères Borwein). Nous proposons
tout de même de partir de cette vieille idée et de calculer les décimales de 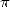 avec
une vitesse que l’on peut choisir aussi grande que désirée (moyennant un calcul
préalable). Ainsi, pour toute valeur de
avec
une vitesse que l’on peut choisir aussi grande que désirée (moyennant un calcul
préalable). Ainsi, pour toute valeur de 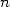 on a la formule qui suit qui demeure
valable:
on a la formule qui suit qui demeure
valable:
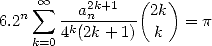 | (3) |
2 Preuve
Nous nous proposons de calculer exactement l’aire hachurée ci-dessous, qui est un secteur du cercle unité.
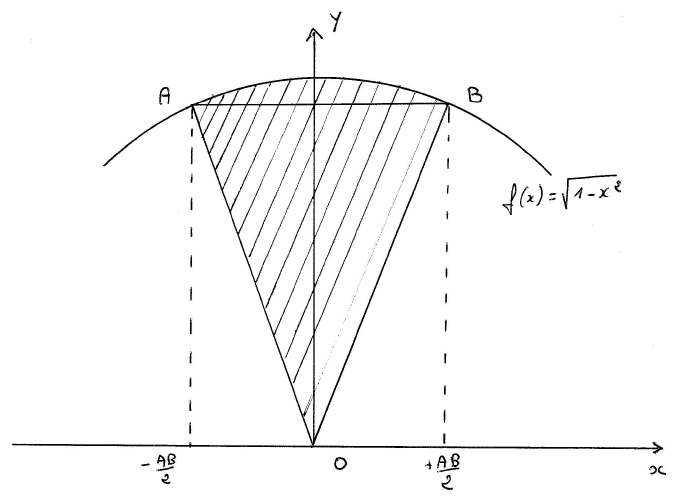
Il est facile de voir que cette surface vaut
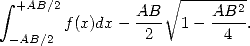 | (4) |
En choisissant 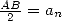 , on a alors pour tout
, on a alors pour tout 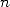 le cercle divisé en secteurs
égaux et :
le cercle divisé en secteurs
égaux et :
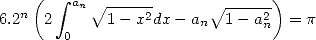 | (5) |
car on retrouve l’aire du cercle unité. D’un autre côté, on a la série connue :
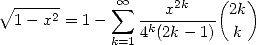 | (6) |
soit 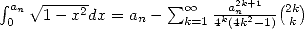 et
et 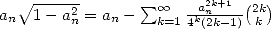 et donc
et donc 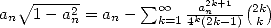 . L’équation 5 devient donc
. L’équation 5 devient donc
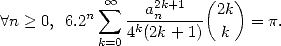 | (7) |
Ceci donne une famille de séries convergeant aussi vite que l’on désire vers 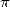 et
améliore donc l’algorithme d’Archimède .
et
améliore donc l’algorithme d’Archimède .
3 Essais
Pour 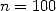 , si on calcule
, si on calcule 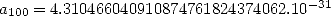 , alors la
série
, alors la
série
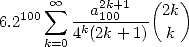 | (8) |
donne environ 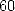 bonnes décimales de
bonnes décimales de 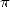 à chaque terme.
à chaque terme.
Autres idées de Benoît Cloitre
Retour à la page d'accueil

 et
et 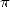 dans un miroir
dans un miroir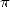 et
et 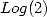 dans un miroir
dans un miroir